【题目】已知圆C的半径为2,圆心在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与圆C相切.
与圆C相切.
(1)求圆C的方程;
(2)过点![]() 的直线
的直线![]() 与圆C交于不同的两点
与圆C交于不同的两点![]() ,且当
,且当![]() 时,求
时,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() +
+![]() (2)
(2)![]()
【解析】试题分析:(I)设圆心为C(a,0),(a>0),可得圆C的方程的方程.再根据圆心到直线的距离等于半径求得a的值,可得圆C的方程.
(II)依题意:设直线l的方程为:y=kx﹣3,代入圆的方程化简,利用根与系数的关系求得两根和与两根积,再由x1x2+y1y2=3,求得k的值,可得∴直线l的方程.求得圆心C到l的距离d、以及|AB|的值,再由面积公式,计算求得结果.
试题解析:
(1)设圆心为![]() ,则圆C的方程为
,则圆C的方程为![]()
因为圆C与![]() 相切 所以
相切 所以![]() 解得:
解得:![]() (舍)
(舍)
所以圆C的方程为:![]()
(2)依题意:设直线l的方程为:![]()
由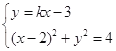 得
得![]()
∵l与圆C相交于不同两点![]()
∴![]()
![]()
![]()
![]()
又∵![]() ∴
∴![]()
整理得:![]() 解得
解得![]() (舍)
(舍)
∴直线l的方程为:![]()
圆心C到l的距离![]() 在△ABC中,|AB|=
在△ABC中,|AB|=![]()
原点O到直线l的距离,即△AOB底边AB边上的高![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
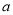 ,
, 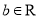 ,函数
,函数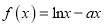 ,
, 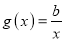 .
.(Ⅰ)若
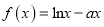 与
与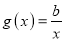 有公共点
有公共点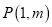 ,且在
,且在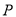 点处切线相同,求该切线方程;
点处切线相同,求该切线方程;(Ⅱ)若函数
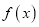 有极值但无零点,求实数
有极值但无零点,求实数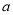 的取值范围;
的取值范围;(Ⅲ)当
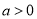 ,
, 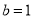 时,求
时,求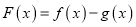 在区间
在区间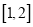 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C经过点
 ,且圆心
,且圆心 在直线
在直线 上,又直线
上,又直线 与圆C交于P,Q两点.
与圆C交于P,Q两点.(1)求圆C的方程;
(2)若
 ,求实数
,求实数 的值;
的值;(3)过点
 作直线
作直线 ,且
,且 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
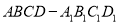 中,
中,  为棱
为棱 上一动点,
上一动点, 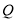 为底面
为底面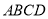 上一动点,
上一动点, 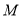 是
是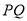 的中点,若点
的中点,若点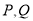 都运动时,点
都运动时,点 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是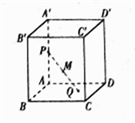
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组
 ,第二组
,第二组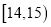 ,…,第五组
,…,第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为
 ,求
,求 的分布列,期望及方差.
的分布列,期望及方差.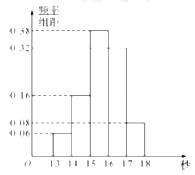
-
科目: 来源: 题型:
查看答案和解析>>【题目】某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )
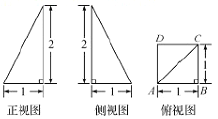
A.
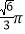 B.
B. 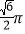 C.
C. 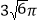 D.
D. 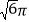
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣
 <α<
<α<  )的最小正周期是π,且当x=
)的最小正周期是π,且当x=  时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
相关试题

