【题目】已知圆C经过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,又直线
上,又直线![]() 与圆C交于P,Q两点.
与圆C交于P,Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数
,求实数![]() 的值;
的值;
(3)过点![]() 作直线
作直线![]() ,且
,且![]() 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形![]() 的面积的最大值.
的面积的最大值.
参考答案:
【答案】(1)x 2 +y 2 =4(2)k=0(3)7
【解析】试题分析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,建立方程,从而可求圆
,建立方程,从而可求圆![]() 的方程;(2)利用向量的数量积公式,求得
的方程;(2)利用向量的数量积公式,求得![]() ,计算圆心到直线
,计算圆心到直线![]() 的距离
的距离![]() ,即可求解实数
,即可求解实数![]() 的值;(3)方法1、设圆
的值;(3)方法1、设圆![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,求得
,求得![]() ,根据垂径定理和勾股定理,可得
,根据垂径定理和勾股定理,可得![]() ,在利用基本不等式,可求四边形
,在利用基本不等式,可求四边形![]() 面积的最大值;方法2、利用弦长公式
面积的最大值;方法2、利用弦长公式![]() ,
, 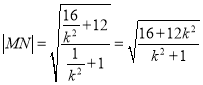 ,表示三角形的面积,在利用基本不等式,可求四边形
,表示三角形的面积,在利用基本不等式,可求四边形![]() 面积的最大值.
面积的最大值.
试题解析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,易得
,易得![]() ,
,
因此圆的方程为![]() .
.
(2)因为![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
故![]() ,
, ![]() ,所以
,所以![]() 到直线
到直线![]() 的距离
的距离![]() ,又
,又![]() ,所以
,所以![]() .
.
又解:设P![]() ,
, ![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,∴
,∴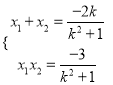 ,
,
代入![]() 得
得![]() ,∴
,∴![]() ;
;
(3)设圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.
因为直线![]() 都经过点
都经过点![]() ,且
,且![]() ,根据勾股定理,有
,根据勾股定理,有![]() ,
,
又![]() ,
,
故![]()
 当且仅当
当且仅当![]() 时,等号成立,所以
时,等号成立,所以![]() .
.
(3)又解:由已知![]() ,由(2)的又解可得
,由(2)的又解可得![]() ,
,
同理可得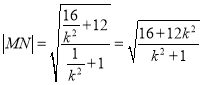 ,
,
∴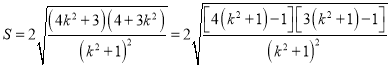
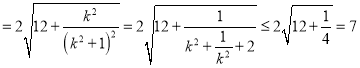 ,
,
当且仅当![]() 时等号成立,所以
时等号成立,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为矩形,
为矩形,  平面
平面 ,
,  ,
,  为
为 中点.
中点.
(I)证明:
 平面
平面 .
.(II)证明:
 平面
平面 .
. -
科目: 来源: 题型:
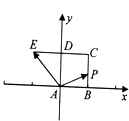
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中
 =λ
=λ 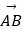 +μ
+μ 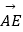 ,则下列命题正确的是 . (填上所有正确命题的序号)
,则下列命题正确的是 . (填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量 和实数x,使
和实数x,使 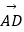 =x
=x 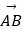 +y
+y 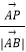 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
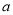 ,
, 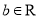 ,函数
,函数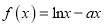 ,
, 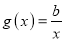 .
.(Ⅰ)若
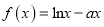 与
与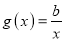 有公共点
有公共点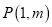 ,且在
,且在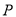 点处切线相同,求该切线方程;
点处切线相同,求该切线方程;(Ⅱ)若函数
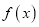 有极值但无零点,求实数
有极值但无零点,求实数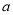 的取值范围;
的取值范围;(Ⅲ)当
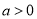 ,
, 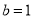 时,求
时,求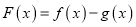 在区间
在区间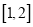 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
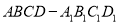 中,
中,  为棱
为棱 上一动点,
上一动点, 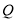 为底面
为底面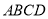 上一动点,
上一动点, 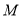 是
是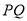 的中点,若点
的中点,若点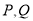 都运动时,点
都运动时,点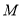 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是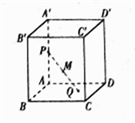
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的半径为2,圆心在
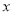 轴的正半轴上,直线
轴的正半轴上,直线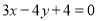 与圆C相切.
与圆C相切.(1)求圆C的方程;
(2)过点
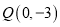 的直线
的直线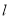 与圆C交于不同的两点
与圆C交于不同的两点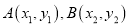 ,且当
,且当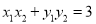 时,求
时,求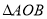 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组
 ,第二组
,第二组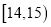 ,…,第五组
,…,第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为
 ,求
,求 的分布列,期望及方差.
的分布列,期望及方差.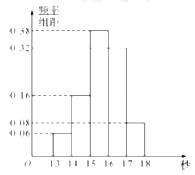
相关试题

