【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
参考答案:
【答案】![]()
【解析】试题分析:(Ⅰ)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(Ⅱ)延长AE至M连结DM,使得AM⊥DM,说明∠CMD=60°,是二面角的平面角,求出CD,即可三棱锥E-ACD的体积
试题解析:(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
因为EO平面AEC,PB平面AEC,
所以PB∥平面AEC.
(2)因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直.
如图,以A为坐标原点, ![]() ,AD,AP的方向为x轴y轴z轴的正方向,|
,AD,AP的方向为x轴y轴z轴的正方向,|![]() |为单位长,建立空间直角坐标系Axyz,则D
|为单位长,建立空间直角坐标系Axyz,则D![]() ,E
,E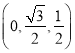 ,
, ![]() =
=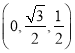 .
.

设B(m,0,0)(m>0),则C(m, ![]() ,0),
,0), ![]() =(m,
=(m, ![]() ,0).
,0).
设n1=(x,y,z)为平面ACE的法向量,
则 即
即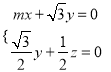
可取n1=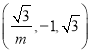 .
.
又n2=(1,0,0)为平面DAE的法向量,
由题设易知|cos〈n1,n2〉|=![]() ,即
,即
![]() =
=![]() ,解得m=
,解得m=![]() .
.
因为E为PD的中点,所以三棱锥EACD的高为![]() .三棱锥EACD的体积V=
.三棱锥EACD的体积V=![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为
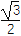 ;
;④f(x)既是奇函数,又是周期函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出
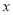 与销售额
与销售额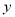 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: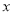
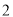
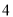
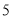
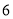
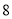
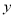
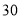
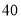
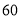
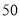
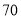
(1)求回归直线方程;
(2)试预测广告费支出为
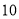 万元时,销售额多大?
万元时,销售额多大?(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过
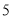 的概率.(参考数据:
的概率.(参考数据: 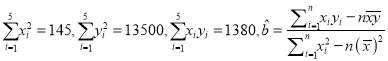 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若
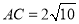 ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.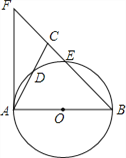
-
科目: 来源: 题型:
查看答案和解析>>【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量x的分布列;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率
相关试题

