Question

【题目】已知等差数列{an}的前n项和为Sn ， 且S3=9，a1 ， a3 ， a7成等比数列．
（1）求数列{an}的通项公式；
（2）若an≠a1时，数列{bn}满足bn=2 ，求数列{bn}的前n项和Tn ．

Answer 1

【答案】
（1）解：∵等差数列{an}的前n项和为Sn，且S3=9，a1，a3，a7成等比数列，

∴ ，解得 或 ，

当 时，an=3；

当 时，an=2+（n﹣1）=n+1

（2）解：∵an≠a1，∴an=n+1，∴bn=2 =2n+1，

∴ ， =2，

∴{bn}是以4为首项，以2为公比的等比数列，

∴Tn= = =2n+2﹣4

【解析】（1）由等差数列前n项和公式、通项公式及等比数列性质，列出方程组，求出首项与公差，由此能求出数列{an}的通项公式．（2）由an≠a1 ， 各bn=2 =2n+1 ， 由此能求出数列{bn}的前n项和Tn ．
【考点精析】本题主要考查了等比数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：；数列{an}的前n项和sn与通项an的关系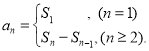才能正确解答此题．