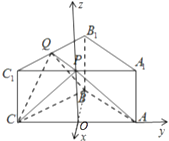
【题目】如图,ABC﹣A1B1C1是底面边长为2,高为 ![]() 的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、
的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、 
(1)证明:PQ∥A1B1;
(2)当 ![]() 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离.
参考答案:
【答案】
(1)证明:∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,
又∵AB∥A1B1,
∴PQ∥A1B1.
(2)解:建立如图所示的直角坐标系.
∴O(0,0,0),P(0,0, ![]() ),A(0,1,0),B(﹣
),A(0,1,0),B(﹣ ![]() ,0,0),C(0,﹣1,0),
,0,0),C(0,﹣1,0),
∴ ![]() =(0,﹣1,
=(0,﹣1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面APQB的法向量为 ![]() =(x,y,z),
=(x,y,z),
则  ,可得
,可得 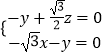 ,
,
取 ![]() =
= ![]() ,
,
∴点C到平面APQB的距离d= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由平面ABC∥平面A1B1C1 , 利用线面平行的性质定理可得:AB∥PQ,又AB∥A1B1 , 即可证明PQ∥A1B1 . (2)建立如图所示的直角坐标系.设平面APQB的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,利用点C到平面APQB的距离d=
,利用点C到平面APQB的距离d= ![]() 即可得出.
即可得出.
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商城一年中各月份的收入、支出(单位:万元)情况的统计如图所示,下列说法正确的是( )

A. 2至3月份的收入的变化率与11至12月份的收入的变化率相同
B. 支出最高值与支出最低值的比是3:1
C. 7至9月的日平均支出为50万元
D. 利润最高的月份是2月份
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , 且S3=9,a1 , a3 , a7成等比数列.
(1)求数列{an}的通项公式;
(2)若an≠a1时,数列{bn}满足bn=2 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(2)商店记录了50天该商品的日需求量(单位:件),整理得表:日需求量n
8
9
10
11
12
频数
10
10
15
10
5
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间[400,550]”为事件A,求P(A)的估计值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的编号为1,2,3,4的球,从袋中随机抽取一个球,将其编号记为m,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为n,则关于x的一元二次方程
 无实根的概率为__________。
无实根的概率为__________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点分别为F1(﹣
 ,0),F2(
,0),F2(  ,0),且椭圆C过点P(3,2).
,0),且椭圆C过点P(3,2).
(1)求椭圆C的标准方程;
(2)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2lnx﹣ax+a(a∈R).
(1)讨论f(x)的单调性;
(2)若f(x)≤0恒成立,证明:当0<x1<x2时, .
.
相关试题

