【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() 且满足
且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求出![]() ,分五种情况讨论
,分五种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)可知,
的减区间;(2)由(1)可知,![]() ,不等式
,不等式![]() 化为
化为![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,利用导数研究函数的单调性,证明当
,利用导数研究函数的单调性,证明当![]() 时,不等式不成立,当
时,不等式不成立,当![]() 时,可证明
时,可证明![]() ,适量题意,即
,适量题意,即![]() .
.
试题解析:(1)定义域为![]() ,
,
![]() ,
,
当![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
于是结合函数定义域的分析可得:
当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上是增函数;
上是增函数;
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是增函数.
上是增函数.
(2)由(1)知![]() 存在两个极值点时,
存在两个极值点时,![]() 的取值范围是
的取值范围是![]() ,
,
由(1)可知,![]() ,
,
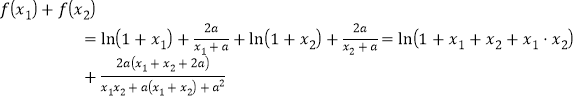
![]() ;
;
不等式![]() 化为
化为![]() ,
,
令![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,适量题意,即
,适量题意,即![]() .
.
综上,若![]() ,此时正数
,此时正数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容易.”这里的“幂”指水平截面的面积.“势”指高,这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。于是可把半径相等的半球(底面在下)和圆柱(圆柱高等于半径)放在同一水平面上,圆柱里再放一个半径和高都与圆柱相等的圆锥(锥尖朝下),考察圆柱里被圆锥截剩的立体,这样在同一高度用平行平面截得的半球截面和圆柱中剩余立体截得的截面面积相等,因此半球的体积等于圆柱中剩余立体的体积.设由椭圆
 所围成的平面图形绕
所围成的平面图形绕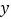 轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.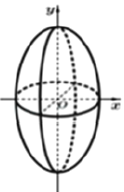
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司
 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.
的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.
(1)由拆线图可以看出,可用线性回归模型拟合月度市场占有率
 与月份代码
与月份代码 之间的关系.求
之间的关系.求 关于
关于 的线性回归方程,并预测
的线性回归方程,并预测 公司2017年4月份(即
公司2017年4月份(即 时)的市场占有率;
时)的市场占有率;(2)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的
 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:车型 报废年限
1年
2年
3年
4年
总计

20
35
35
10
100

10
30
40
20
100
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年,且以频率作为每辆单车使用寿命的概率.如果你是
 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?(参考公式:回归直线方程为
 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,侧棱
中,侧棱 垂直于底面
垂直于底面 ,
, ,
, ,
, 为
为 的中点,
的中点, 平行于
平行于 ,
, 平行于面
平行于面 ,
, .
.
(1)求
 的长;
的长;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量 (单位:
(单位: )和年利润
)和年利润 (单位:千元)的影响,对近13年的宣传费
(单位:千元)的影响,对近13年的宣传费 和年销售量
和年销售量
 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
由散点图知,按
 建立
建立 关于
关于 的回归方程是合理的.令
的回归方程是合理的.令 ,则
,则 ,经计算得如下数据:
,经计算得如下数据:






10.15
109.94
0.16
-2.10
0.21
21.22
(1)根据以上信息,建立
 关于
关于 的回归方程;
的回归方程;(2)已知这种产品的年利润
 与
与 的关系为
的关系为 .根据(1)的结果,求当年宣传费
.根据(1)的结果,求当年宣传费 时,年利润的预报值是多少?
时,年利润的预报值是多少?附:对于一组数据
 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若
 在定义域上是增函数,求
在定义域上是增函数,求 的取值范围;
的取值范围;(2)若存在
 ,使得
,使得 ,求
,求 的值,并说明理由.
的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 是参数).以坐标原点为极点,
是参数).以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的直角坐标方程和
的直角坐标方程和 的普通方程;
的普通方程;(2)
 与
与 相交于
相交于 两点,设点
两点,设点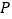 为
为 上异于
上异于 的一点,当
的一点,当 面积最大时,求点
面积最大时,求点 到
到 的距离.
的距离.
相关试题

