【题目】某校高二(20)班共50名学生,在期中考试中,每位同学的数学考试分数都在区间![]() 内,将该班所有同学的考试分数分为七个组:
内,将该班所有同学的考试分数分为七个组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制出频率分布直方图如图所示.
,绘制出频率分布直方图如图所示.

(1)根据频率分布直方图,估计这次考试学生成绩的中位数和平均数;
(2)已知成绩为104分或105分的同学共有3人,现从成绩在![]() 中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数)
中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数)
参考答案:
【答案】(1)中位数为114,平均数为114.32;(2)![]()
【解析】
(Ⅰ)根据中位数的两边概率相等,即可求出中位数;由每组的中间值乘以该组的频率再求和即可求出平均数;
(Ⅱ)先由题意求出成绩在![]() 的人数,对成绩为104分或105分的同学和成绩为106分、107分的学生编号,用列举法结合古典概型的概率计算公式即可求出结果.
的人数,对成绩为104分或105分的同学和成绩为106分、107分的学生编号,用列举法结合古典概型的概率计算公式即可求出结果.
(Ⅰ)由频率分布直方图,知![]() ,所以学生成绩的中位数为
,所以学生成绩的中位数为![]() .
.
平均数为![]()
![]() .
.
(Ⅱ)因为![]() ,所以成绩在
,所以成绩在![]() 之间的学生共有6人.
之间的学生共有6人.
设成绩为104分、105分的学生为![]() ,
,![]() ,
,![]() ,成绩为106分、107分的学生为
,成绩为106分、107分的学生为![]() ,
,![]() ,
,![]() .从6人中任选2人,共有
.从6人中任选2人,共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 15种情况,其中恰好2人都不低于106分的有
15种情况,其中恰好2人都不低于106分的有![]() ,
,![]() ,
,![]() 共3种情况,其中有1人不低于106分1人低于106分的有
共3种情况,其中有1人不低于106分1人低于106分的有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共9人,所以从成绩在
共9人,所以从成绩在![]() 中的同学中任选2人,则至少有1人成绩都不低于106分的概率为
中的同学中任选2人,则至少有1人成绩都不低于106分的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,
, 是
是 的中点,以
的中点,以 为折痕将
为折痕将 向上折起,
向上折起, 变为
变为 ,且平面
,且平面 平面
平面 .
.
(Ⅰ)求证:
 ;
;(Ⅱ)求点
 到平面
到平面 的距离
的距离 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数

 一段图象如图所示。
一段图象如图所示。
(1)求出函数
 的解析式;
的解析式; (2) 函数
 的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到?
的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到? (3) 求出
 的单调递增区间;
的单调递增区间;(4) 指出当
 取得最小值时
取得最小值时 的集合.
的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
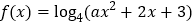
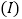 若
若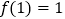 ,求
,求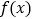 的单调区间;
的单调区间;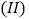 是否存在实数a,使
是否存在实数a,使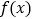 的最小值为0?若存在,求出a的值;若不存在,说明理由.
的最小值为0?若存在,求出a的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

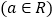 .
.(Ⅰ)当
 时,求
时,求 的图象在
的图象在 处的切线方程;
处的切线方程;(Ⅱ)若函数
 与
与 图象在
图象在 上有两个不同的交点,求实数
上有两个不同的交点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图(1)所示的四边形
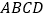 中,
中,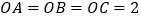 ,
,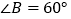 ,
,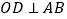 ,
,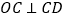 .将
.将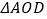 沿
沿 折起,使二面角
折起,使二面角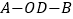 为直二面角(如图(2)),
为直二面角(如图(2)),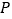 为
为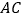 的中点.
的中点.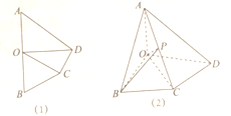
(1)求证:
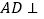 平面
平面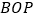 ;
;(2)求二面角
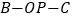 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 均为奇函数,且
均为奇函数,且 在
在 上的最大值为
上的最大值为 ,则在
,则在 上
上 的最小值为__________.
的最小值为__________.
相关试题

