【题目】已知![]() ,
,![]() 均为奇函数,且
均为奇函数,且![]() 在
在![]() 上的最大值为
上的最大值为![]() ,则在
,则在![]() 上
上![]() 的最小值为__________.
的最小值为__________.
参考答案:
【答案】-1
【解析】
根据定义得出f(﹣x)+f(x)=0,g(﹣x)+g(x)=0,即F(x)+F(﹣x)=4,根据F(x)图象关于(0,2)对称,求解得出F(x)在(﹣∞,0)上的最小值F(﹣x0)=4﹣5=﹣1.
∵f(x)和g(x)都是定义域在R上的奇函数,若F(x)=af(x)+bg(x)+2,
则F(x)﹣2=af(x)+bg(x)为奇函数,
∵f(﹣x)+f(x)=0,g(﹣x)+g(x)=0,
∴F(x)+F(﹣x)=4,
F(x)图象关于(0,2)对称,
∵在(0,+∞)上有最大值为5,
∴最大值为F(x0)=5,
即F(x)在(﹣∞,0)上的最小值F(﹣x0)=4﹣5=﹣1.
故F(x)在(﹣∞,0)上的最小值为﹣1,
故答案为:﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二(20)班共50名学生,在期中考试中,每位同学的数学考试分数都在区间
 内,将该班所有同学的考试分数分为七个组:
内,将该班所有同学的考试分数分为七个组: ,
, ,
, ,
, ,
, ,
, ,
, ,绘制出频率分布直方图如图所示.
,绘制出频率分布直方图如图所示.
(1)根据频率分布直方图,估计这次考试学生成绩的中位数和平均数;
(2)已知成绩为104分或105分的同学共有3人,现从成绩在
 中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数)
中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

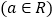 .
.(Ⅰ)当
 时,求
时,求 的图象在
的图象在 处的切线方程;
处的切线方程;(Ⅱ)若函数
 与
与 图象在
图象在 上有两个不同的交点,求实数
上有两个不同的交点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图(1)所示的四边形
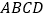 中,
中,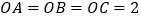 ,
,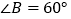 ,
,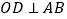 ,
,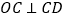 .将
.将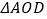 沿
沿 折起,使二面角
折起,使二面角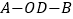 为直二面角(如图(2)),
为直二面角(如图(2)),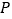 为
为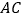 的中点.
的中点.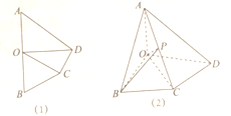
(1)求证:
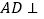 平面
平面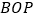 ;
;(2)求二面角
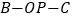 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
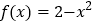 ,
, .
.(Ⅰ)若
 ,解不等式
,解不等式 ;
;(Ⅱ)若不等式
 至少有一个负数解,求实数
至少有一个负数解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
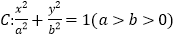 的右焦点为
的右焦点为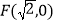 ,
,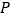 为圆
为圆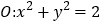 与椭圆
与椭圆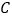 的一个公共点,
的一个公共点,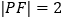 .
.
(Ⅰ)求椭圆
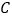 的标准方程;
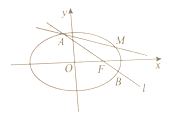
的标准方程;(Ⅱ)如图,过
 作直线
作直线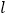 与椭圆
与椭圆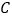 交于
交于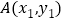 ,
,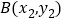 两点,点
两点,点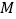 为点
为点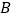 关于
关于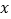 轴的对称点.
轴的对称点.(1)求证:
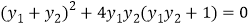 ;
;(2)试问过
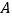 ,
,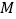 的直线是否过定点?若是,请求出该定点;若不是,请说明理由.
的直线是否过定点?若是,请求出该定点;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近
 ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当 时,
时,  是
是 的二次函数;当
的二次函数;当 时,
时,  .测得部分数据如表.
.测得部分数据如表.x(单位:克)
0
1
2
9
…
y
0

3

…
(1)求y关于x的函数关系式y=

(2)求函数
 的最大值
的最大值
相关试题

