【题目】学校高一数学考试后,对![]() 分(含
分(含![]() 分)以上的成绩进行统计,其频率分布直方图如图所示,分数在
分)以上的成绩进行统计,其频率分布直方图如图所示,分数在![]() 分的学生人数为
分的学生人数为![]() 人,
人,

(1)求这所学校分数在![]() 分的学生人数;
分的学生人数;
(2)请根据频率发布直方图估计这所学校学生分数在![]() 分的学生的平均成绩;
分的学生的平均成绩;
(3)为进“步了解学生的学习情况,按分层抽样方法从分数在![]() 分和
分和![]() 分的学生中抽出
分的学生中抽出![]() 人,从抽出的学生中选出
人,从抽出的学生中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,求
,求![]() 分的学生做问卷
分的学生做问卷![]() ,
,![]() 分的学生做问卷
分的学生做问卷![]() 的概率.
的概率.
参考答案:
【答案】(1)200人;(2)113分;(3)![]() .
.
【解析】试题分析:(1)由分数在120~130分的学生人数为30人,且分数在120~130分频率为0.15,能求出分数在90~140分的学生人数.
(2)由频率分布直方图能估计这所学校学生分数在90~140分的学生的平均成绩.
(3)分数在90~100分的学生人数为20人,分数在120~130分的学生人数为30人,按照分层抽样方法抽出5人时,从分数在90~100分的学生抽出2人,记为A1,A2,从分数在![]() 分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
试题解析:
(1)![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人,且分数在
人,且分数在![]() 分频率为
分频率为![]() ,
,![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
(2)估计这所学校学生分数在![]() 分的学生的平均成绩为
分的学生的平均成绩为
![]() 分.
分.
(3)因为分数在![]() 分的学生人数为
分的学生人数为![]() 人,分数在
人,分数在![]() 分的学生人数为
分的学生人数为![]() 人,所以按分层抽样方法抽出
人,所以按分层抽样方法抽出![]() 人时,分数在
人时,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() ,分数在
,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() .从抽出
.从抽出![]() 人中选出
人中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,共有
,共有![]() 种情况,分别为
种情况,分别为![]() , 设事件
, 设事件![]() “
“![]() 分的学生做问卷
分的学生做问卷![]() ,
,![]() 分的学生做问卷
分的学生做问卷![]() ”,则事件
”,则事件![]() 共有
共有![]() 种情况,分别为
种情况,分别为![]() ,
,![]() ,即事件
,即事件![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
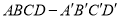 的底面
的底面 是菱形,
是菱形,  ,
, 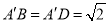 ,
, 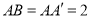 .
.(Ⅰ)证明:平面
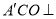 平面
平面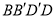 ;
;(Ⅱ)若
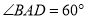 ,直线
,直线 上是否存在点
上是否存在点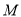 ,使得
,使得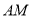 与平面
与平面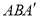 所成角的正弦值为
所成角的正弦值为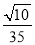 .若存在,求
.若存在,求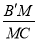 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.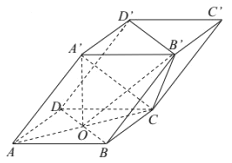
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,圆心为
,圆心为 ,定点
,定点 ,
,  为圆
为圆 上一点,线段
上一点,线段 上一点
上一点 满足
满足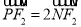 ,直线
,直线 上一点
上一点 ,满足
,满足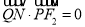 .
.(Ⅰ)求点
 的轨迹
的轨迹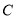 的方程;
的方程;(Ⅱ)
 为坐标原点,
为坐标原点,  是以
是以 为直径的圆,直线
为直径的圆,直线 与
与 相切,并与轨迹
相切,并与轨迹 交于不同的两点
交于不同的两点 .当
.当 且满足
且满足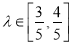 时,求
时,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了
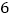 个试销售数据,得到第
个试销售数据,得到第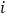 个销售单价
个销售单价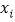 (单位:元)与销售
(单位:元)与销售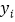 (单位:件)的数据资料,算得
(单位:件)的数据资料,算得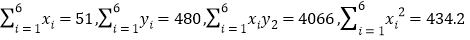
(1)求回归直线方程
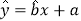 ;
;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是
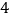 元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)
元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)附:回归直线方程
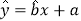 中,
中, ,其中
,其中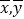 是样本平均值.
是样本平均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是
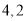 ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为 的正方形.
的正方形.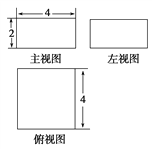
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
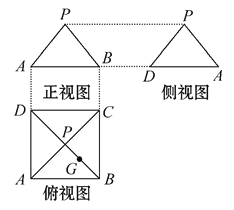
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
相关试题

