【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
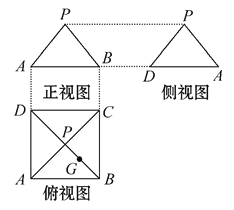
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据三视图,可得该几何体为正四棱锥![]() ,正方形
,正方形![]() 的边长为2,正四棱锥的高为
的边长为2,正四棱锥的高为![]() ,由此可得该几何体的直观图.
,由此可得该几何体的直观图.
(Ⅱ)①在直观图中,设正方形![]() 的中心为
的中心为![]() ,利用三角形的中位线证明
,利用三角形的中位线证明![]() .再由直线和平面平行的判定定理证得
.再由直线和平面平行的判定定理证得![]() 面
面![]() .
.
②连接![]() ,则
,则![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,即可求此几何体的侧面积.
,即可求此几何体的侧面积.
试题解析:(1)该几何体的直观图如图所示.
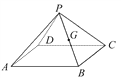
(2)如图,①连接AC,BD交于点O,连接OG,
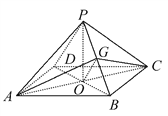
因为G为PB的中点,O为BD的中点,所以OG∥PD,又OG平面AGC,PD平面AGC,所以PD∥平面AGC.
②连接PO,由三视图,PO⊥平面ABCD,所以AO⊥PO.又AO⊥BO,BO∩PO=O,所以AO⊥平面PBD,因为AO平面AGC,所以平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
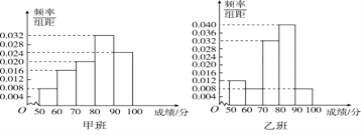
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
甲班(A方式)
乙班(B方式)
总计
成绩优秀
成绩不优秀
总计
附:.
P(K2≥k)
0.25
0.15
0.10
0.05
0.025
k
1.323
2.072
2.706
3.841
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5
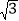 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
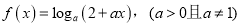
(1)设
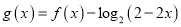 ,当
,当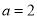 时,求函数
时,求函数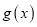 的定义域,判断并证明函数
的定义域,判断并证明函数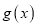 的奇偶性;
的奇偶性;(2)是否存在实数
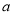 ,使得函数
,使得函数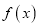 在
在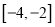 递减,并且最小值为1,若存在,求出
递减,并且最小值为1,若存在,求出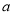 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义在
是定义在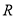 上的奇函数,且当
上的奇函数,且当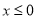 时,
时, 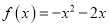 ;
;(1)求函数
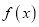 在
在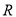 上的解析式并画出函数
上的解析式并画出函数 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)(2)(ⅰ)写出函数
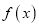 的单调递增区间;
的单调递增区间;(ⅱ)若方程
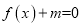 在
在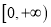 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数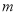 的取值范围。
的取值范围。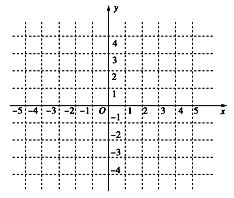
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
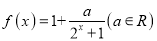 .
.(1)当
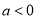 时,判断并证明函数
时,判断并证明函数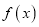 在
在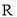 上单调性。
上单调性。(2)当
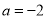 时,若关于
时,若关于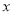 的方程
的方程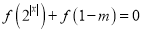 在
在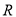 上有解,求实数
上有解,求实数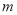 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
相关试题

