【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) 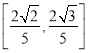 .
.
【解析】试题分析:(Ⅰ)分析题意可得点![]() 满足的几何条件,根据椭圆的定义可得轨迹,从而可求得轨迹方程;(Ⅱ)先由直线
满足的几何条件,根据椭圆的定义可得轨迹,从而可求得轨迹方程;(Ⅱ)先由直线![]() 与
与![]() 相切得到
相切得到![]() ,将直线方程与椭圆方程联立,并结合一元二次方程根与系数的关系可得
,将直线方程与椭圆方程联立,并结合一元二次方程根与系数的关系可得![]() ,由
,由![]() 且
且![]() ,进一步得到k的范围,最后根据三角形面积公式并结合函数的单调性求
,进一步得到k的范围,最后根据三角形面积公式并结合函数的单调性求![]() 的取值范围。
的取值范围。
试题解析:
(Ⅰ)∵![]()
∴![]() 为线段
为线段![]() 中点
中点
∵![]()
∴![]() 为线段
为线段![]() 的中垂线
的中垂线
∴![]()
∵![]()
∴由椭圆的定义可知![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
设椭圆的标准方程为![]() ,
,
则![]() ,
, ![]() ,
,
∴![]() 。
。
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() 。
。
(Ⅱ)∵圆![]() 与直线
与直线![]() 相切,
相切,
∴![]() ,即
,即![]() ,
,
由 ,消去
,消去![]() .
.
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴![]() ,
,
将![]() 代入上式,可得
代入上式,可得![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
∴![]()
![]() ,
,
∴
∴![]() ,
,
∵![]() ,解得
,解得![]() .满足
.满足![]() 。
。
又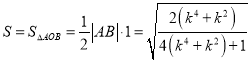 ,
,
设![]() ,则
,则![]() .
.
∴![]()
 ,
,
∴![]()
故![]() 面积
面积![]() 的取值范围为
的取值范围为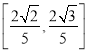 。
。
-
科目: 来源: 题型:
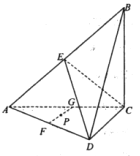
查看答案和解析>>【题目】如图,在四面体
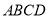 中,平面
中,平面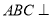 平面
平面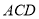 ,
, 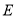 ,
, 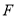 ,
, 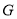 分别为
分别为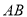 ,
, 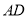 ,
, 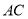 的中点,
的中点, 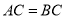 ,
, 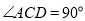 .
.(1)求证:
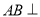 平面
平面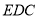 ;
;(2)若
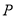 为
为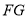 上任一点,证明
上任一点,证明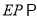 平面
平面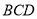 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
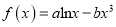 ,
, 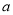 ,
, 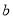 为实数,
为实数, 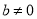 ,
, 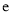 为自然对数的底数,
为自然对数的底数, 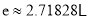 .
.(1)当
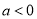 ,
, 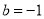 时,设函数
时,设函数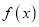 的最小值为
的最小值为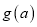 ,求
,求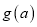 的最大值;
的最大值;(2)若关于
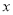 的方程
的方程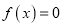 在区间
在区间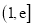 上有两个不同实数解,求
上有两个不同实数解,求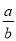 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x,y满足约束条件:
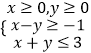 ;则z=x﹣2y的取值范围为 .
;则z=x﹣2y的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第
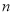 局得
局得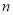 分(
分(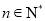 )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数
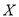 的分布列和数学期望
的分布列和数学期望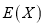 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某科研小组研究发现:一棵水蜜桃树的产量
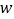 (单位:百千克)与肥料费用
(单位:百千克)与肥料费用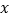 (单位:百元)满足如下关系:
(单位:百元)满足如下关系: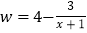 ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)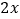 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为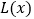 (单位:百元).
(单位:百元).(1)求利润函数
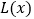 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
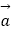 =(sinx,sin(x﹣
=(sinx,sin(x﹣  )),
)), 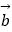 =(sinx,cos(x+
=(sinx,cos(x+  )),f(x)=
)),f(x)= 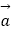
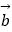 .
.
(1)求f(x)的解析式及周期;
(2)求f(x)在x∈[﹣ ,
,  ]上的值域.
]上的值域.
相关试题

