【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
参考答案:
【答案】
(1)解:f(x)=(x+l)lnx﹣ax+a,f′(x)=lnx+ ![]() +1﹣a,
+1﹣a,
若f(x)在(0,+∞)上单调递增,
则a≤lnx+ ![]() +1在(0,+∞)恒成立,(a>0),
+1在(0,+∞)恒成立,(a>0),
令g(x)=lnx+ ![]() +1,(x>0),
+1,(x>0),
g′(x)= ![]() ,
,
令g′(x)>0,解得:x>1,令g′(x)<0,解得:0<x<1,
故g(x)在(0,1)递减,在(1,+∞)递增,
故g(x)min=g(1)=2,
故0<a≤2;
(2)解:若不等式(x﹣1)f(x)≥0恒成立,
即(x﹣1)[(x+1)lnx﹣a]≥0恒成立,
①x≥1时,只需a≤(x+1)lnx恒成立,
令m(x)=(x+1)lnx,(x≥1),
则m′(x)=lnx+ ![]() +1,
+1,
由(1)得:m′(x)≥2,
故m(x)在[1,+∞)递增,m(x)≥m(1)=0,
故a≤0,而a为正实数,故a≤0不合题意;
②0<x<1时,只需a≥(x+1)lnx,
令n(x)=(x+1)lnx,(0<x<1),
则n′(x)=lnx+ ![]() +1,由(1)n′(x)在(0,1)递减,
+1,由(1)n′(x)在(0,1)递减,
故n′(x)>n(1)=2,
故n(x)在(0,1)递增,故n(x)<n(1)=0,
故a≥0,而a为正实数,故a>0.
【解析】(1)求出函数f(x)的导数,问题转化为a≤lnx+ ![]() +1在(0,+∞)恒成立,(a>0),令g(x)=lnx+
+1在(0,+∞)恒成立,(a>0),令g(x)=lnx+ ![]() +1,(x>0),根据函数的单调性求出a的范围即可;(2)问题转化为(x﹣1)[(x+1)lnx﹣a]≥0恒成立,通过讨论x的范围,结合函数的单调性求出a的范围即可.
+1,(x>0),根据函数的单调性求出a的范围即可;(2)问题转化为(x﹣1)[(x+1)lnx﹣a]≥0恒成立,通过讨论x的范围,结合函数的单调性求出a的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一数学考试后,对
 分(含
分(含 分)以上的成绩进行统计,其频率分布直方图如图所示,分数在
分)以上的成绩进行统计,其频率分布直方图如图所示,分数在 分的学生人数为
分的学生人数为 人,
人,
(1)求这所学校分数在
 分的学生人数;
分的学生人数;(2)请根据频率发布直方图估计这所学校学生分数在
 分的学生的平均成绩;
分的学生的平均成绩;(3)为进“步了解学生的学习情况,按分层抽样方法从分数在
 分和
分和 分的学生中抽出
分的学生中抽出 人,从抽出的学生中选出
人,从抽出的学生中选出 人分别做问卷
人分别做问卷 和问卷
和问卷 ,求
,求 分的学生做问卷
分的学生做问卷 ,
, 分的学生做问卷
分的学生做问卷 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是
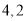 ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为 的正方形.
的正方形.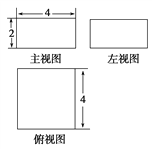
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
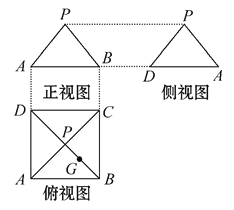
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是:从装有
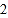 个红球
个红球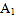 ,
,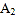 和
和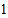 个白球
个白球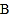 的甲箱与装有
的甲箱与装有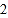 个红球
个红球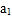 ,
,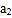 和
和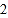 个白球
个白球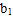 ,
,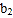 的乙箱中,各随机摸出
的乙箱中,各随机摸出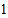 个球,若模出的
个球,若模出的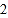 个球都是红球则中奖,否则不中奖.
个球都是红球则中奖,否则不中奖.(1)用球的标号列出所有可能的模出结果;
(2)有人认为:两个箱子中的红球比白球多所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
 中,四边形
中,四边形 为矩形,
为矩形,  为等腰三角形,
为等腰三角形,  ,平面
,平面 平面
平面 ,且
,且 ,
, 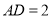 ,
,  分别为
分别为 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)证明:平面
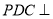 平面
平面 ;
;(3)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
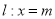 (
(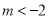 )与
)与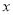 轴交于
轴交于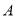 点,动圆
点,动圆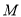 与直线
与直线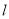 相切,并且与圆
相切,并且与圆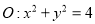 相外切,
相外切,(1)求动圆的圆心
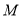 的轨迹
的轨迹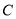 的方程;
的方程;(2)若过原点且倾斜角为
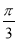 的直线与曲线
的直线与曲线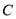 交于
交于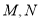 两点,问是否存在以
两点,问是否存在以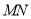 为直径的圆经过点
为直径的圆经过点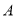 ?若存在,求出
?若存在,求出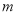 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

