【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
,![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
,![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
试题分析:(1)有曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]()
(![]() 为参数),消去参数的
为参数),消去参数的![]() 是圆,
是圆,![]() 是椭圆,并利用.当
是椭圆,并利用.当![]() 时,这两个交点间的距离为
时,这两个交点间的距离为![]() ,当
,当![]() 时,这两个交点重合,求出
时,这两个交点重合,求出![]() 及
及![]() .(2)利用
.(2)利用![]() 的普通方程,当
的普通方程,当![]() 时,
时,![]() 与
与![]() 的交点分别为
的交点分别为![]() ,当
,当![]() 时,
时,![]() 与
与![]() 的交点为
的交点为![]() ,利用面积公式求出面积.
,利用面积公式求出面积.
试题解析:(1)![]() 是圆,
是圆,![]() 是椭圆.
是椭圆.
当![]() 时,射线
时,射线![]() 与
与![]() ,
,![]() 交点的直角坐标分别是
交点的直角坐标分别是![]() 因为这两点间的距离为2,所以
因为这两点间的距离为2,所以![]()
当![]() ,射线
,射线![]() 与
与![]() ,
,![]() 交点的直角坐标分别是
交点的直角坐标分别是![]() 因为这两点重合,所以
因为这两点重合,所以![]() ;
;
(2)![]() ,
,![]() 的普通方程为
的普通方程为![]()
当![]() 时,射线
时,射线![]() 与
与![]() 交点
交点![]() 的横纵表是
的横纵表是![]() ,与
,与![]() 交点
交点![]() 的横坐标是
的横坐标是![]()
当![]() 时,射线
时,射线![]() 与
与![]() ,
,![]() 的两个交点
的两个交点![]() 分别与交点
分别与交点![]() 关于
关于![]() 轴对称,因此四边形
轴对称,因此四边形![]() 为梯形,故四边形
为梯形,故四边形![]() 的面积为
的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,则x1+x2的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
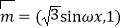 ,
,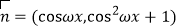 ,设函数
,设函数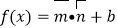 .
.(1)若函数
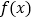 的图象关于直线
的图象关于直线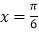 对称,且
对称,且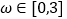 时,求函数
时,求函数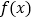 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
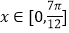 时,函数
时,函数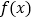 有且只有一个零点,求实数
有且只有一个零点,求实数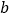 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
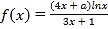 ,曲线
,曲线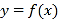 在点
在点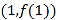 处的切线与直线
处的切线与直线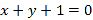 垂直.
垂直.(1)求
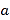 的值;
的值;(2)若对于任意的
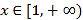 ,
, 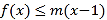 恒成立,求
恒成立,求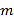 的取值范围;
的取值范围;(3)求证:
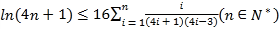 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=
 (a∈R).
(a∈R).(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
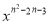 (n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
(n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
相关试题

