【题目】已知函数y=![]() (n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
(n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
参考答案:
【答案】n=-1或n=1或n=3,此时解析式为y=x0(x≠0)或y=x-4(x≠0),图像见解析
【解析】试题分析:由题意可得,可得幂指数![]() 为负数,可得
为负数,可得![]() ,且为偶数,讨论
,且为偶数,讨论 ![]() 时,幂指数
时,幂指数![]() 是否为偶数,可得
是否为偶数,可得![]() 合题意,分别代入可得函数的解析式,从而得到函数的图象.
合题意,分别代入可得函数的解析式,从而得到函数的图象.
试题解析:因为图像与x轴无交点,所以n2-2n-3≤0,又图像关于y轴对称,则n2-2n-3为偶数.
由n2-2n-3≤0,得-1≤n≤3,又n∈Z,所以n=0,±1,2,3.
当n=0时,n2-2n-3=-3不是偶数;
当n=1时,n2-2n-3=-4是偶数;
当n=-1时,n2-2n-3=0是偶数;
当n=2时,n2-2n-3=-3不是偶数;
当n=3时,n2-2n-3=0是偶数.
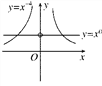
综上,n=-1或n=1或n=3,此时解析式为y=x0(x≠0)或y=x-4(x≠0),如图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
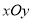 中,曲线
中,曲线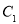 的参数方程为
的参数方程为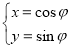 (
(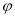 为参数),曲线
为参数),曲线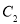 的参数方程为
的参数方程为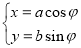 (
(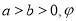 为参数),在以
为参数),在以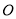 为极点,
为极点,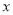 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线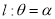 ,与
,与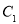 ,
,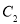 各有一个交点,当
各有一个交点,当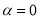 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当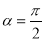 ,这两个交点重合.
,这两个交点重合.(1)分别说明
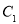 ,
,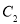 是什么曲线,并求出
是什么曲线,并求出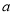 与
与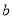 的值;
的值;(2)设当
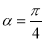 时,
时,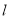 与
与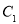 ,
,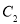 的交点分别为
的交点分别为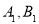 ,当
,当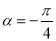 ,
,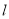 与
与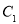 ,
,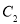 的交点分别为
的交点分别为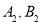 ,求四边形
,求四边形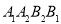 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
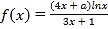 ,曲线
,曲线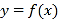 在点
在点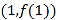 处的切线与直线
处的切线与直线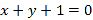 垂直.
垂直.(1)求
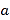 的值;
的值;(2)若对于任意的
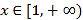 ,
, 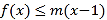 恒成立,求
恒成立,求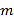 的取值范围;
的取值范围;(3)求证:
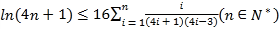 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=
 (a∈R).
(a∈R).(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份
2012年
2013年
2014
2015
2016
广告投入x
0.8
0.9
1
1.1
1.2
销售收入y
16
23
25
26
30
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
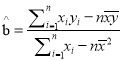
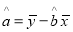 ,选用数据:
,选用数据: 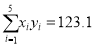 ,
, 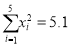
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数
 ,其中
,其中
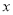 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润 总收益
总收益 总成本.
总成本.(1)试将自行车厂的利润
 元表示为月产量
元表示为月产量 的函数;
的函数;(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数),每人每年可创利b万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
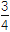 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
相关试题

