【题目】设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)若对于任意的![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)详见解析
(Ⅲ)详见解析
【解析】试题分析:(Ⅰ)先求导数,再根据导数几何意义列方程,解方程可得![]() 的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数:
的值;(Ⅱ)不等式恒成立问题,一般转化为对应函数最值问题,本题去分母转化为差函数: ![]() ,因为
,因为![]() ,所以
,所以![]() 最大值不小于
最大值不小于![]() ,根据
,根据![]() 导函数符号可得
导函数符号可得![]() 才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当
才满足条件.(Ⅲ)不等式证明中涉及求和问题,一般方法为适当放缩,再利用裂项相消法给予证明.本题由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立,所以放缩这一难点已暗示,下面只需令
成立,所以放缩这一难点已暗示,下面只需令![]() 得
得![]() ,即
,即![]() ,最后叠加可得证.
,最后叠加可得证.
试题解析:(Ⅰ) 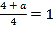
由题设![]() ,∴
,∴![]()
![]() .
.
(Ⅱ)![]() ,
,![]() ,
, ![]() ,即
,即![]()
设![]() ,即
,即![]() .
.
![]()
![]()
①若![]() ,
, ![]() ,这与题设
,这与题设![]() 矛盾
矛盾
②若![]() 当
当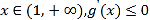 ,
, ![]() 单调递增,
单调递增, ![]() ,与题设矛盾.
,与题设矛盾.
③若![]() 当
当![]() ,
, ![]() 单调递减,
单调递减, ![]() ,即不等式成立
,即不等式成立
综上所述, ![]() .
.
(Ⅲ)由(Ⅱ)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立.
成立.
不妨令![]() 所以
所以![]() ,
,
![]()
![]()
![]()
…………
![]()
累加可得
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
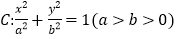 经过点
经过点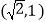 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
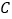 的方程;
的方程;(Ⅱ)设
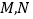 是椭圆上的点,直线
是椭圆上的点,直线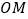 与
与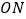 (
(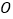 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为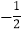 .若动点
.若动点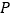 满足
满足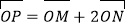 ,试探究是否存在两个定点
,试探究是否存在两个定点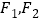 ,使得
,使得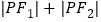 为定值?若存在,求
为定值?若存在,求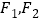 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
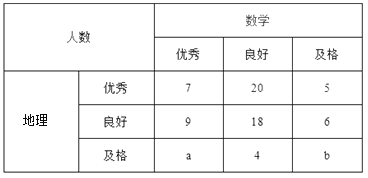
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有
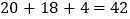 .
.(Ⅰ)若在该样本中,数学成绩优秀率是30%,求
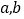 的值;
的值;(Ⅱ)已知
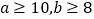 ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
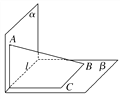
A. 30° B. 45°
C. 60° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.
(I)求X的分布列和数学期望
 ;
;(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设
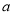 表示王老师某月每个工作日出行的平均费用,若
表示王老师某月每个工作日出行的平均费用,若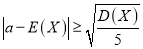 ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:
,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
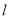 与圆C:
与圆C: 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),(1)求实数
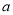 的取值范围以及直线
的取值范围以及直线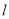 的方程;
的方程;(2)若圆C上存在四个点到直线
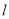 的距离为
的距离为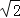 ,求实数a的取值范围;
,求实数a的取值范围;(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使
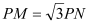 ,求实数
,求实数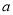 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
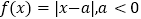 .
.(1)证明:
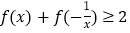 ;
;(2)若不等式
 的解集是非空集,求
的解集是非空集,求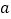 的范围.
的范围.
相关试题

