【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据平面向量数量积运算求解出函数![]() ,利用函数
,利用函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 可得
可得![]() ,结合三角函数的性质可得其单调区间;(2)当
,结合三角函数的性质可得其单调区间;(2)当![]() 时,求出函数
时,求出函数![]() 的单调性,函数
的单调性,函数![]() 有且只有一个零点,利用其单调性求解求实数
有且只有一个零点,利用其单调性求解求实数![]() 的取值范围.
的取值范围.
试题解析:
解:向量![]() ,
,![]() ,
,
![]()
![]()
(1)∵函数![]() 图象关于直线
图象关于直线![]() 对称,
对称,
∴![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,由
,由![]() ,
,
解得:![]() ,
,
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
(2)由(1)知![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;
单调递增;
![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减.
单调递减.
又![]() ,
,
∴当![]() 或
或![]() 时函数
时函数![]() 有且只有一个零点.
有且只有一个零点.
即![]() 或
或![]() ,
,
所以满足条件的![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
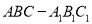 中,
中, 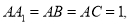
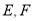 分别是
分别是 的中点, 且
的中点, 且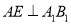 ,
,(1)证明:
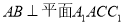 .
.(2)棱
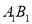 上是否存在一点
上是否存在一点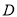 ,使得平面
,使得平面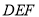 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为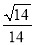 若存在,说明点
若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.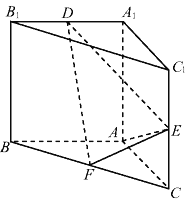
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,则x1+x2的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线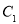 的参数方程为
的参数方程为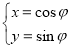 (
(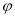 为参数),曲线
为参数),曲线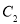 的参数方程为
的参数方程为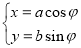 (
(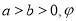 为参数),在以
为参数),在以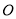 为极点,
为极点,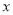 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线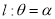 ,与
,与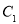 ,
,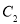 各有一个交点,当
各有一个交点,当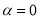 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当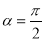 ,这两个交点重合.
,这两个交点重合.(1)分别说明
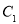 ,
,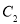 是什么曲线,并求出
是什么曲线,并求出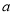 与
与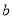 的值;
的值;(2)设当
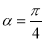 时,
时,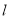 与
与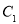 ,
,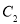 的交点分别为
的交点分别为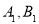 ,当
,当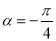 ,
,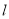 与
与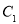 ,
,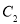 的交点分别为
的交点分别为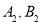 ,求四边形
,求四边形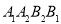 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
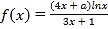 ,曲线
,曲线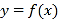 在点
在点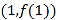 处的切线与直线
处的切线与直线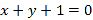 垂直.
垂直.(1)求
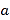 的值;
的值;(2)若对于任意的
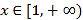 ,
, 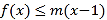 恒成立,求
恒成立,求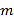 的取值范围;
的取值范围;(3)求证:
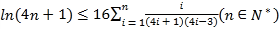 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=
 (a∈R).
(a∈R).(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
相关试题

