【题目】已知函数 ![]() .
.
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在 ![]() 上的值域是
上的值域是 ![]() ,求a的值.
,求a的值.
参考答案:
【答案】
(1)证明:证明:设x2>x1>0,则x2﹣x1>0,x1x2>0,
∵ 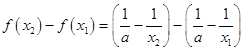 =
= ![]() ,
,
∴f(x2)>f(x1),
∴f(x)在(0,+∞)上是单调递增的
(2)证明:∵f(x)在(0,+∞)上是单调递增的,
∴f(x)在 ![]() 上单调递增,
上单调递增,
∴ ![]() ,
,
∴ ![]()
【解析】(1)利用函数单调性的定义,设x2>x1>0,再将f(x1)﹣f(x2)作差后化积,证明即可;(2)由(1)知f(x)在(0,+∞)上是单调递增的,从而在[ ![]() ,2]上单调递增,由f(2)=2可求得a的值.
,2]上单调递增,由f(2)=2可求得a的值.
【考点精析】掌握函数单调性的判断方法和函数单调性的性质是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0且a≠1,下列四组函数中表示相等函数的是( )
A.y=logax与y=(logxa)﹣1
B.y=2x与y=logaa2x
C.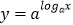 与y=x
与y=x
D.y=logax2与y=2logax -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为集合A,y=﹣x2+2x+2a的值域为B.
的定义域为集合A,y=﹣x2+2x+2a的值域为B.
(1)若a=2,求A∩B
(2)若A∪B=R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=f(x)最大值为3,且f(﹣4)=f(0)=﹣1
(1)求f(x)的解析式;
(2)求f(x)在[﹣3,3]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1﹣x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为﹣4,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,以坐标原点为极点,
中,以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆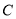 的极坐标方程为
的极坐标方程为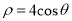 .
.(1)求出圆
 的直角坐标方程;
的直角坐标方程;(2)已知圆
 与
与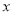 轴相交于
轴相交于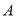 ,
, 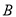 两点,直线
两点,直线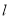 :
: 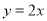 关于点
关于点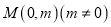 对称的直线为
对称的直线为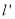 .若直线
.若直线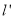 上存在点
上存在点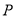 使得
使得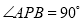 ,求实数
,求实数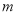 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 中,
中, 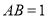 ,
, 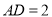 ,点
,点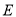 为
为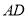 中点,沿
中点,沿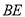 将
将 折起至
折起至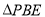 ,如下图所示,点
,如下图所示,点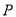 在面
在面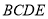 的射影
的射影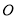 落在
落在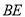 上.
上.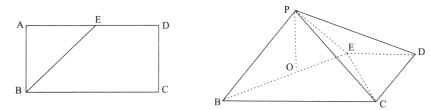
(Ⅰ)求证:
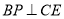 ;
;(Ⅱ)求二面角
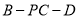 的余弦值.
的余弦值.
相关试题

