【题目】已知函数f(x)=loga(1﹣x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为﹣4,求a的值.
参考答案:
【答案】
(1)解:要使函数有意义:则有 ![]() ,解之得:﹣3<x<1,
,解之得:﹣3<x<1,
则函数的定义域为:(﹣3,1)
(2)解:函数可化为f(x)=loga(1﹣x)(x+3)=loga(﹣x2﹣2x+3)
由f(x)=0,得﹣x2﹣2x+3=1,
即x2+2x﹣2=0, ![]()
∵ ![]() ,∴函数f(x)的零点是
,∴函数f(x)的零点是 ![]()
(3)解:函数可化为:
f(x)=loga(1﹣x)(x+3)=loga(﹣x2﹣2x+3)=loga[﹣(x+1)2+4]
∵﹣3<x<1,∴0<﹣(x+1)2+4≤4,
∵0<a<1,∴loga[﹣(x+1)2+4]≥loga4,
即f(x)min=loga4,由loga4=﹣4,得a﹣4=4,
∴ ![]()
【解析】(1)根据对数的真数大于零,列出不等式组并求出解集,函数的定义域用集合或区间表示出来;(2)利用对数的运算性质对解析式进行化简,再由f(x)=0,即﹣x2﹣2x+3=1,求此方程的根并验证是否在函数的定义域内;(3)把函数解析式化简后,利用配方求真数在定义域内的范围,再根据对数函数在定义域内递减,求出函数的最小值loga4,得loga4=﹣4利用对数的定义求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为集合A,y=﹣x2+2x+2a的值域为B.
的定义域为集合A,y=﹣x2+2x+2a的值域为B.
(1)若a=2,求A∩B
(2)若A∪B=R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=f(x)最大值为3,且f(﹣4)=f(0)=﹣1
(1)求f(x)的解析式;
(2)求f(x)在[﹣3,3]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在 上的值域是
上的值域是  ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
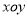 中,以坐标原点为极点,
中,以坐标原点为极点, 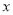 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆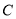 的极坐标方程为
的极坐标方程为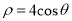 .
.(1)求出圆
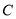 的直角坐标方程;
的直角坐标方程;(2)已知圆
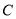 与
与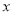 轴相交于
轴相交于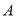 ,
, 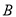 两点,直线
两点,直线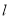 :
: 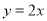 关于点
关于点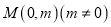 对称的直线为
对称的直线为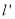 .若直线
.若直线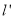 上存在点
上存在点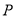 使得
使得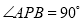 ,求实数
,求实数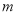 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
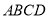 中,
中, 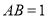 ,
, 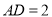 ,点
,点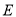 为
为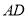 中点,沿
中点,沿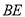 将
将 折起至
折起至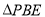 ,如下图所示,点
,如下图所示,点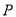 在面
在面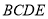 的射影
的射影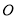 落在
落在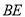 上.
上.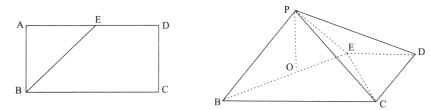
(Ⅰ)求证:
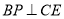 ;
;(Ⅱ)求二面角
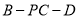 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=
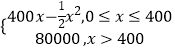 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
相关试题

