【题目】已知![]() .
.
(Ⅰ)若![]() 在
在![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)令![]() ,若函数
,若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ) ![]() 在
在![]() 是单调递增函数,等价于
是单调递增函数,等价于![]() 在
在![]() 上恒成立,再转化为
上恒成立,再转化为![]() ,求最值即可.
,求最值即可.
(Ⅱ)![]()
![]() 有两个零点,可转化为
有两个零点,可转化为![]()
![]() ,有两个交点问题,用导数研究函数的增减变化情况即可.
,有两个交点问题,用导数研究函数的增减变化情况即可.
试题解析:(Ⅰ)由题意知![]() ,
,
![]() .
.
![]() 在
在![]() 是单调递增函数
是单调递增函数
![]() 在
在![]() 上恒成立
上恒成立
![]() ,
,
![]() .
.
(Ⅱ)由题意知![]()
![]() ,
,
由![]()
![]()
![]() ,
,
令![]()
![]() ,
,
![]() ,
,
由于![]() ,可知
,可知![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上是单调减函数,
上是单调减函数,
在![]() 上是单调增函数,所以
上是单调增函数,所以![]() ,
,
函数![]() 有两个零点
有两个零点![]() ,
,
因此实数a的取值范围是![]() .
.
点晴:本题考查函数导数与单调性.确定零点的个数问题:可利用数形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车
不同意限定区域停车
合计
男
18
7
25
女
12
13
25
合计
30
20
50
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为
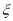 ,求
,求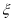 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
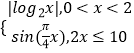 ,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则
,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则 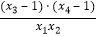 的取值范围是( )
的取值范围是( )
A.(20,32)
B.(9,21)
C.(8,24)
D.(15,25) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-k)ex,
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
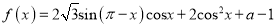 .
.(Ⅰ)求
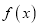 的最小正周期;
的最小正周期;(Ⅱ)若
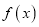 在区间
在区间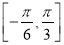 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求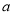 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知θ∈[0,
 ],直线xsinθ+ycosθ﹣1=0和圆C:(x﹣1)2+(y﹣cosθ)2=
],直线xsinθ+ycosθ﹣1=0和圆C:(x﹣1)2+(y﹣cosθ)2=  相交所得的弦长为
相交所得的弦长为 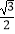 ,则θ= .
,则θ= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是函数f(x)=
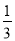 ax3-
ax3-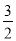 x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
相关试题

