【题目】已知函数![]() .
.
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)若![]() 在区间
在区间![]() 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据二倍角公式及辅助角公式可将函数化为![]() 即可求得周期 ;(Ⅱ)根据三角函数的有界性不,求出函数的最值,列方程求解即可.
即可求得周期 ;(Ⅱ)根据三角函数的有界性不,求出函数的最值,列方程求解即可.
试题解析:(Ⅰ) ![]()
![]()
![]()
![]()
![]()
(Ⅱ)因为![]() ,所以
,所以![]()
当![]() ,即
,即![]() 时,
时, ![]() 单调递增
单调递增
当![]() ,即
,即![]() 时,
时, ![]() 单调递减
单调递减
所以![]()
又因为![]() ,
, ![]()
所以![]()
故![]() ,因此
,因此![]()
【方法点晴】本题主要考查三角函数的单调性、三角函数的周期性及三角函数的有界性,属于难题.三角函数的图象与性质是高考考查的热点之一,经常考查定义域、值域、周期性、对称性、奇偶性、单调性、最值等,其中公式运用及其变形能力、运算能力、方程思想等可以在这些问题中进行体现,在复习时要注意基础知识的理解与落实.三角函数的性质由函数的解析式确定,在解答三角函数性质的综合试题时要抓住函数解析式这个关键,在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式,然后利用正弦(余弦)函数的性质求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
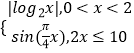 ,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则
,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则 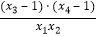 的取值范围是( )
的取值范围是( )
A.(20,32)
B.(9,21)
C.(8,24)
D.(15,25) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-k)ex,
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
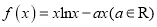 .
.(Ⅰ)若
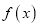 在
在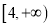 是单调递增函数,求实数
是单调递增函数,求实数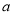 的取值范围;
的取值范围;(Ⅱ)令
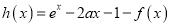 ,若函数
,若函数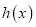 有两个零点,求实数
有两个零点,求实数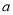 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知θ∈[0,
 ],直线xsinθ+ycosθ﹣1=0和圆C:(x﹣1)2+(y﹣cosθ)2=
],直线xsinθ+ycosθ﹣1=0和圆C:(x﹣1)2+(y﹣cosθ)2=  相交所得的弦长为
相交所得的弦长为 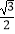 ,则θ= .
,则θ= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是函数f(x)=
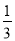 ax3-
ax3-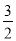 x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 :
: 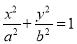 (
(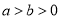 )的左右焦点分别为
)的左右焦点分别为 ,
, 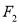 ,下顶点为
,下顶点为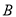 ,直线
,直线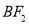 的方程为
的方程为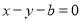 .
.(Ⅰ)求椭圆
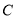 的离心率;
的离心率;(Ⅱ)设
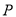 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, 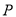 到直线
到直线 的距离为
的距离为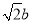 ,且三角形
,且三角形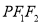 的面积为
的面积为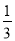 .
.(1)求椭圆
 的方程;
的方程;(2)若斜率为
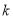 的直线
的直线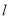 与椭圆
与椭圆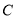 相切,过焦点
相切,过焦点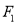 ,
, 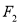 分别作
分别作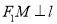 ,
, 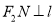 ,垂足分别为
,垂足分别为 ,
,  ,求
,求 的最大值.
的最大值.
相关试题

