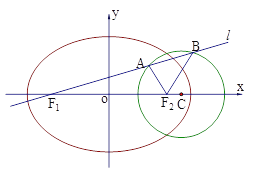
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.
(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)
;(Ⅱ) ![]() 为定值,其值为2.
为定值,其值为2.
【解析】试题分析:(Ⅰ)通过计算圆心和半径得圆的方程,根据![]() 计算a的值,及焦点得c即可得椭圆方程;
计算a的值,及焦点得c即可得椭圆方程;
(Ⅱ)由直线和椭圆联立,利用韦达定理,利用坐标表示![]() ,计算即可定值.
,计算即可定值.
试题解析:
(Ⅰ)依题意知圆C的半径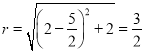 ,
,
∴圆C的标准方程为: ![]() ;
;
∵椭圆![]() 过点M
过点M![]() ,且焦点为
,且焦点为![]() 、
、![]() ,
,
由椭圆的定义得: ![]() ,
,
即![]() ,
,
∴![]() ,
, ![]() ,
,
∴椭圆E的方程为: ![]() .
.
【其它解法请参照给分】
(Ⅱ)显然直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
由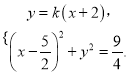 消去
消去![]() 得:
得:
![]() ,
,
显然![]() 有解,
有解,
设![]() 、
、![]() ,则
,则![]() ,
,
![]()
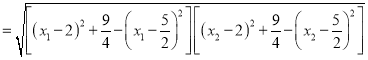
![]() .
.
故![]() 为定值,其值为2.
为定值,其值为2.
-
科目: 来源: 题型:
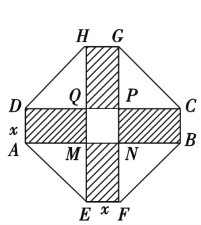
查看答案和解析>>【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致为( )
A.
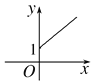 B.
B.  C.
C. 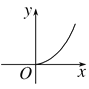 D.
D. 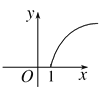
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy上取两个定点
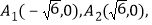 再取两个动点
再取两个动点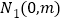 ,
,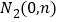 ,且
,且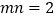 .
.(Ⅰ)求直线
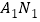 与
与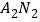 交点M的轨迹C的方程;
交点M的轨迹C的方程;(Ⅱ)过
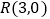 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作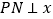 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若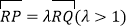 ,求证:
,求证: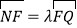 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)选修4—5:不等式选讲
已知
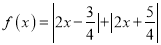 .
.(1)关于
 的不等式
的不等式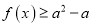 恒成立,求实数
恒成立,求实数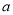 的取值范围;
的取值范围;(2)设
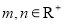 ,且
,且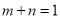 ,求证:
,求证: 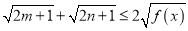 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
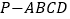 中,底面
中,底面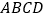 是长方形,侧棱
是长方形,侧棱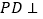 底面
底面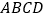 ,且
,且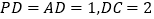 ,过D作
,过D作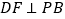 于F,过F作
于F,过F作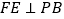 交 PC于E.
交 PC于E.(Ⅰ)证明:
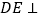 平面PBC;
平面PBC;(Ⅱ)求平面
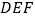 与平面
与平面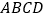 所成二面角的余弦值.
所成二面角的余弦值. 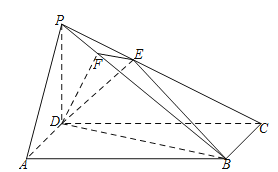
相关试题

