【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】【试题分析】(Ⅰ)先建立动直线的方程,再运用消参法探求轨迹方程; (Ⅱ)借助直线与椭圆的位置关系推证:
(Ⅰ)依题意知直线A1N1的方程为![]() ①
①
直线A2N2的方程为![]() ②………………………………2分
②………………………………2分
设M(x,y)是直线A1N1与A2N2交点,①×②得 ![]() ,
,
由mn=2,整理得![]() ; ………………………………4分
; ………………………………4分
(Ⅱ)设![]() ,
,![]()
由 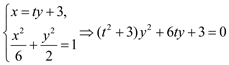 (
(![]() ) ………………………………6分
) ………………………………6分
由![]() 故
故![]() , ………………8分
, ………………8分
要证![]() ,即证
,即证![]() ,只需证:
,只需证:![]()
只需![]() 即证
即证 ![]() 即
即![]() ,………10分
,………10分
由(![]() )得:
)得:![]() ,即证. ……………………12分
,即证. ……………………12分
(本题亦可先证直线NQ过焦点F,再由![]() 得证)
得证)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
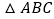 中,角
中,角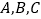 的对边分别为
的对边分别为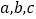 ,
,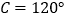 .
.(Ⅰ)若
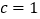 ,求
,求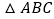 面积的最大值;
面积的最大值;(Ⅱ)若
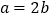 ,求
,求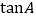 .
.
-
科目: 来源: 题型:
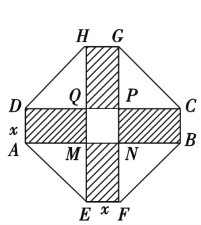
查看答案和解析>>【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致为( )
A.
 B.
B.  C.
C. 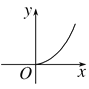 D.
D. 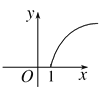
-
科目: 来源: 题型:
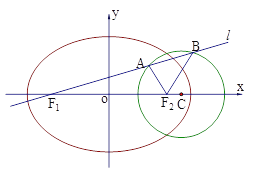
查看答案和解析>>【题目】已知如图,圆
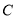 、椭圆
、椭圆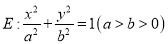 均经过点M
均经过点M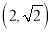 ,圆
,圆 的圆心为
的圆心为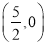 ,椭圆
,椭圆 的两焦点分别为
的两焦点分别为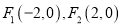 .
.
(Ⅰ)分别求圆
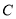 和椭圆
和椭圆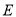 的标准方程;
的标准方程; (Ⅱ)过
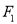 作直线
作直线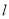 与圆
与圆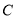 交于
交于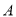 、
、 两点,试探究
两点,试探究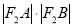 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)选修4—5:不等式选讲
已知
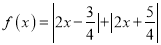 .
.(1)关于
 的不等式
的不等式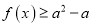 恒成立,求实数
恒成立,求实数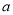 的取值范围;
的取值范围;(2)设
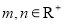 ,且
,且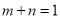 ,求证:
,求证: 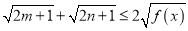 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
相关试题

