【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
参考答案:
【答案】见解析
【解析】
(1)证明 求函数f(x)的导数
f′(x)=ax2-2bx+2-b.
由函数f(x)在x=x1处取得极大值,
在x=x2处取得极小值,
知x1、x2是f′(x)=0的两个根,
所以f′(x)=a(x-x1)(x-x2).
当x<x1时,f(x)为增函数,f′(x)>0,
由x-x1<0,x-x2<0得a>0.
(2)解 在题设下,0<x1<1<x2<2等价于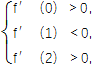
即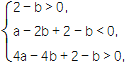 化简得
化简得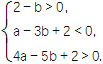
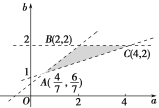
此不等式组表示的区域为平面aOb上的三条直线:
2-b=0,a-3b+2=0,4a-5b+2=0所围成的△ABC的内部,其三个顶点分别为A![]() ,B(2,2),C(4,2).
,B(2,2),C(4,2).
z在这三点的值依次为![]() ,6,8.
,6,8.
所以z的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy上取两个定点
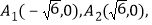 再取两个动点
再取两个动点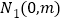 ,
,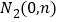 ,且
,且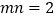 .
.(Ⅰ)求直线
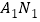 与
与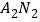 交点M的轨迹C的方程;
交点M的轨迹C的方程;(Ⅱ)过
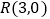 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作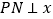 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若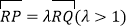 ,求证:
,求证: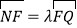 .
. -
科目: 来源: 题型:
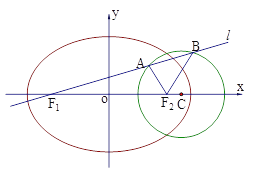
查看答案和解析>>【题目】已知如图,圆
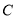 、椭圆
、椭圆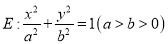 均经过点M
均经过点M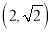 ,圆
,圆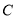 的圆心为
的圆心为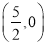 ,椭圆
,椭圆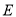 的两焦点分别为
的两焦点分别为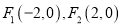 .
.
(Ⅰ)分别求圆
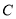 和椭圆
和椭圆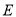 的标准方程;
的标准方程; (Ⅱ)过
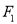 作直线
作直线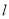 与圆
与圆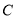 交于
交于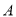 、
、 两点,试探究
两点,试探究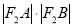 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)选修4—5:不等式选讲
已知
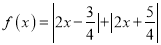 .
.(1)关于
 的不等式
的不等式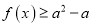 恒成立,求实数
恒成立,求实数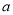 的取值范围;
的取值范围;(2)设
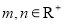 ,且
,且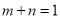 ,求证:
,求证: 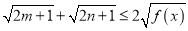 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
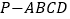 中,底面
中,底面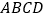 是长方形,侧棱
是长方形,侧棱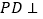 底面
底面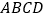 ,且
,且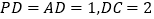 ,过D作
,过D作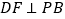 于F,过F作
于F,过F作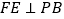 交 PC于E.
交 PC于E.(Ⅰ)证明:
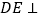 平面PBC;
平面PBC;(Ⅱ)求平面
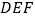 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值. 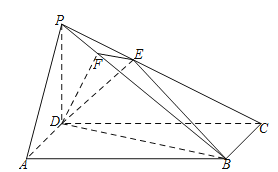
-
科目: 来源: 题型:
查看答案和解析>>【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度
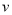 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度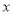 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当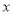 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,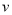 的值为
的值为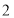 (千克/年);当
(千克/年);当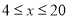 时,
时,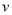 是
是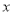 的一次函数;当
的一次函数;当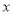 达到
达到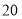 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,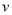 的值为
的值为 (千克/年).
(千克/年).(1)当
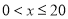 时,求函数
时,求函数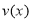 的表达式;
的表达式;(2)当养殖密度
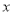 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)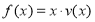 可以达到最大,并求出最大值.
可以达到最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
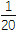 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
相关试题

