【题目】(本小题满分10分)选修4—5:不等式选讲
已知![]() .
.
(1)关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)不等式![]() 恒成立,不等式或两个字母
恒成立,不等式或两个字母![]() 与
与![]() 是分离的,因此有
是分离的,因此有![]() 小于或等于
小于或等于![]() 最小值,由绝对值的几何意义可求得
最小值,由绝对值的几何意义可求得![]() 的最小值(
的最小值(![]() 表示数轴上的点
表示数轴上的点![]() 与点
与点![]() 和点
和点![]() 的距离之和,最小值为2),解不等式
的距离之和,最小值为2),解不等式![]() 即得
即得![]() 的取值范围;(2)问题实质上就是证明不等式
的取值范围;(2)问题实质上就是证明不等式![]() ,观察已知发现当
,观察已知发现当![]() 时,等号成立,由此我们凑出基本不等式,即
时,等号成立,由此我们凑出基本不等式,即![]() ,结论得证.
,结论得证.
试题解析:(1)依据绝对值的几何意义可知函数![]() 表示数轴上点P(
表示数轴上点P(![]() )到点A(
)到点A(![]() )和B(
)和B(![]() )两点的距离,其最小值为
)两点的距离,其最小值为![]()
∴不等式恒成立只需![]() ,解得
,解得![]()
(2)∵![]() ∴只需证明:
∴只需证明: ![]() 成立即可.
成立即可.
![]() ;
; ![]() .
.
于是![]()
∴![]()
故要证明的不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某林区的森林蓄积量每年比上一年平均增长9.5%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图像大致为( )
A.
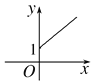 B.
B.  C.
C. 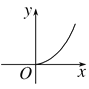 D.
D. 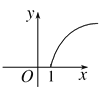
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy上取两个定点
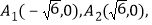 再取两个动点
再取两个动点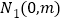 ,
,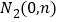 ,且
,且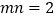 .
.(Ⅰ)求直线
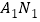 与
与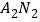 交点M的轨迹C的方程;
交点M的轨迹C的方程;(Ⅱ)过
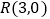 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作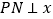 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若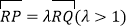 ,求证:
,求证: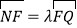 .
. -
科目: 来源: 题型:
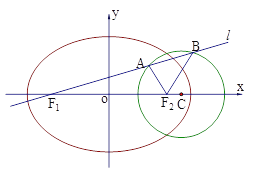
查看答案和解析>>【题目】已知如图,圆
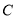 、椭圆
、椭圆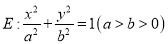 均经过点M
均经过点M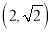 ,圆
,圆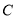 的圆心为
的圆心为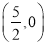 ,椭圆
,椭圆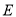 的两焦点分别为
的两焦点分别为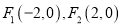 .
.
(Ⅰ)分别求圆
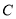 和椭圆
和椭圆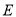 的标准方程;
的标准方程; (Ⅱ)过
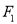 作直线
作直线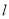 与圆
与圆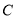 交于
交于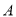 、
、 两点,试探究
两点,试探究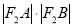 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
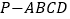 中,底面
中,底面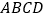 是长方形,侧棱
是长方形,侧棱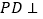 底面
底面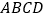 ,且
,且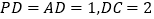 ,过D作
,过D作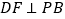 于F,过F作
于F,过F作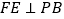 交 PC于E.
交 PC于E.(Ⅰ)证明:
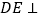 平面PBC;
平面PBC;(Ⅱ)求平面
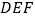 与平面
与平面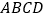 所成二面角的余弦值.
所成二面角的余弦值. 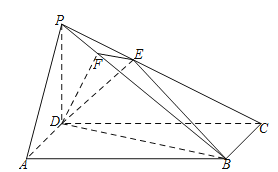
-
科目: 来源: 题型:
查看答案和解析>>【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度
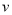 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度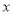 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当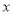 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,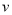 的值为
的值为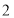 (千克/年);当
(千克/年);当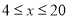 时,
时,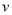 是
是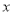 的一次函数;当
的一次函数;当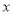 达到
达到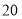 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,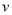 的值为
的值为 (千克/年).
(千克/年).(1)当
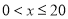 时,求函数
时,求函数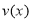 的表达式;
的表达式;(2)当养殖密度
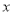 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)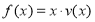 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
相关试题

