【题目】已知递增等比数列{an}的第三项、第五项、第七项的积为512,且这三项 分别减去1,3,9后成等差数列.
(1)求{an}的首项和公比;
(2)设Sn=a12+a22+…+an2 , 求Sn .
参考答案:
【答案】
(1)解:根据等比数列的性质,可得a3a5a7=a53=512,解之得a5=8.
设数列{an}的公比为q,则a3= ![]() ,a7=8q2,
,a7=8q2,
由题设可得( ![]() ﹣1)+(8q2﹣9)=2(8﹣3)=10
﹣1)+(8q2﹣9)=2(8﹣3)=10
解之得q2=2或 ![]() .
.
∵{an}是递增数列,可得q>1,∴q2=2,得q= ![]() .
.
因此a5=a1q4=4a1=8,解得a1=2
(2)解:由(1)得{an}的通项公式为an=a1qn﹣1=2× ![]() =
= ![]() ,
,
∴an2=[ ![]() ]2=2n+1,
]2=2n+1,
可得{an2}是以4为首项,公比等于2的等比数列.
因此Sn=a12+a22+…+an2= ![]() =2n+2﹣4
=2n+2﹣4
【解析】(1)根据题意利用等比数列的性质,可得a53=512,解出a5=8.设公比为q,得a3= ![]() 且a7=8q2 , 由等差中项的定义建立关于q的方程,解出q的值,进而可得{an}的首项;(2)由(1)得an=a1qn﹣1=
且a7=8q2 , 由等差中项的定义建立关于q的方程,解出q的值,进而可得{an}的首项;(2)由(1)得an=a1qn﹣1= ![]() ,从而得到an2=[
,从而得到an2=[ ![]() ]2=2n+1 , 再利用等比数列的求和公式加以计算,可得求Sn的表达式.
]2=2n+1 , 再利用等比数列的求和公式加以计算,可得求Sn的表达式.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an} 中,已知公差
 ,且a1+a3+a5+…+a99=60,则a1+a2+a3+…+a100= .
,且a1+a3+a5+…+a99=60,则a1+a2+a3+…+a100= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m2与3m2 . 用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个.问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}、{bn}满足:a1=
 ,an+bn=1,bn+1=
,an+bn=1,bn+1= 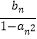 .
.
(1)求a2 , a3;
(2)证数列{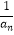 }为等差数列,并求数列{an}和{bn}的通项公式;
}为等差数列,并求数列{an}和{bn}的通项公式;
(3)设Sn=a1a2+a2a3+a3a4+…+anan+1 , 求实数λ为何值时4λSn<bn恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为( )
A.130
B.170
C.210
D.260 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c满足b2+c2﹣a2=bc,
 ,
,  ,则b+c的取值范围是( )
,则b+c的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
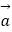 =(1,0),
=(1,0), 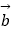 =(2,1).
=(2,1).
(1)求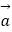 +3
+3 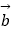 的坐标;
的坐标;
(2)当k为何实数时,k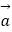 ﹣
﹣ 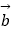 与
与 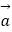 +3
+3 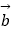 平行,平行时它们是同向还是反向?
平行,平行时它们是同向还是反向?
相关试题

