【题目】已知 ![]() =(1,0),
=(1,0), ![]() =(2,1).
=(2,1).
(1)求 ![]() +3
+3 ![]() 的坐标;
的坐标;
(2)当k为何实数时,k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,平行时它们是同向还是反向?
平行,平行时它们是同向还是反向?
参考答案:
【答案】
(1)解:∵ ![]() =(1,0),
=(1,0), ![]() =(2,1).
=(2,1).
∴ ![]() +3
+3 ![]() =(1,0)+(6,3)=(7,3)
=(1,0)+(6,3)=(7,3)
(2)解:k ![]() ﹣
﹣ ![]() =(k﹣2,﹣1),
=(k﹣2,﹣1), ![]() +3
+3 ![]() =(7,3),
=(7,3),
∵k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,∴3(k﹣2)+7=0,解得k=﹣
平行,∴3(k﹣2)+7=0,解得k=﹣ ![]() .
.
∴k ![]() ﹣
﹣ ![]() =
= ![]() ,
, ![]() +3
+3 ![]() =(7,3),
=(7,3),
∴k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,方向相反
平行,方向相反
【解析】(1)利用向量坐标运算性质即可得出.(2)利用向量共线定理即可得出.
【考点精析】关于本题考查的平面向量的坐标运算,需要了解坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知递增等比数列{an}的第三项、第五项、第七项的积为512,且这三项 分别减去1,3,9后成等差数列.
(1)求{an}的首项和公比;
(2)设Sn=a12+a22+…+an2 , 求Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为( )
A.130
B.170
C.210
D.260 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c满足b2+c2﹣a2=bc,
 ,
,  ,则b+c的取值范围是( )
,则b+c的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷,卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数
 是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入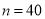 ,则输出的结果为( )
,则输出的结果为( )
A. 120 B. 121 C. 112 D. 113
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}满足a3=5,a10=﹣9.
(1)求数列{an}的通项公式;
(2)求Sn的最大值及其相应的n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若把函数y=sin(ωx﹣
 )的图象向左平移
)的图象向左平移  个单位,所得到的图象与函数y=cosωx的图象重合,则ω的一个可能取值是( )
个单位,所得到的图象与函数y=cosωx的图象重合,则ω的一个可能取值是( )
A.2
B.
C.
D.
相关试题

