【题目】已知函数![]() .
.
(I)求函数![]() 在
在![]() 上的最值;
上的最值;
(II)已知函数![]() ,求证:
,求证:![]() ,
,![]() 恒成立.
恒成立.
参考答案:
【答案】(I)![]() ,
,![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】
试题分析:(I)借助题设条件运用导数的知识求解;(II)借助题设构造函数运用导数的知识分析推证.
试题解析:
(I)![]() 的定义域为
的定义域为![]() ,............................1分
,............................1分
![]() 恒成立对
恒成立对![]() ,............................2分
,............................2分
![]() 在
在![]() 上递增,
上递增,![]() ,
,![]() ...............4分
...............4分
(II)证明:令![]() ;............................5分
;............................5分
![]() 在
在![]() 上恒成立,............7分
上恒成立,............7分
![]() 在区间
在区间![]() 上递减,............................................................8分
上递减,............................................................8分
![]() ,......................................................10分
,......................................................10分
![]() 在区间
在区间![]() 上,
上,![]() 恒成立............................................12分
恒成立............................................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱
 中,
中,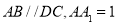 ,
,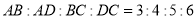 ,侧棱
,侧棱 底面
底面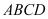 .
.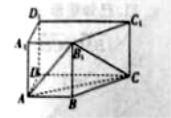
(I)证明:平面
 平面
平面 ;
;(II)若直线
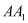 与平面
与平面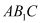 所成的角的余弦值为
所成的角的余弦值为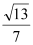 ,求
,求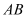 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是
 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是 ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是 .
.(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
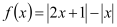 .
.(I)求证:
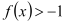 恒成立;
恒成立;(II)若存在实数
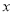 ,使得
,使得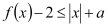 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
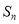 为等差数列
为等差数列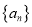 的前
的前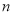 项和,且
项和,且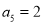 ,
, 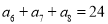 .
.(1)求数列
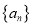 的通项公式;
的通项公式;(2)若
 ,求证:
,求证: 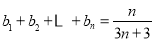 ;
;(3)求数列
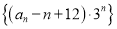 的前
的前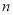 项和
项和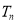 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】陕西省洛川地处北纬35°-36°,东经109°,昼夜温差
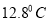 ,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用
,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用 (万元)与销售额
(万元)与销售额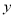 (万元)之间有下面对应数据:
(万元)之间有下面对应数据: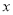
2
4
5
6
8
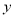
30
40
60
50
70
(1)假设
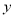 与
与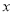 之间线性相关,求回归直线方程;
之间线性相关,求回归直线方程;(2)预测广告和包装费用为10(万元)时销售额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
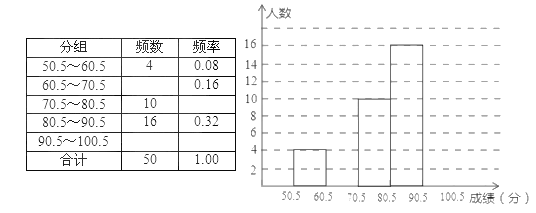
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
相关试题

