【题目】如图,在直四棱柱![]() 中,
中,![]() ,
,
![]() ,侧棱
,侧棱![]() 底面
底面![]() .
.
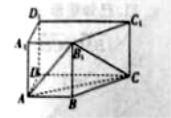
(I)证明:平面![]() 平面
平面![]() ;
;
(II)若直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ,求
,求![]() .
.
参考答案:
【答案】(I)证明见解析;(II)![]() .
.
【解析】
试题分析:(I)借助题设条件运用面面垂直的判定定理推证;(II)借助题设建立空间坐标系运用向量的数量积公式探求.
试题解析:
(I)证明:过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
则![]() 是平行四边形,
是平行四边形,![]() ..........................2分
..........................2分
在![]() 中,因为
中,因为![]() ,
,
所以![]() ......................................................4分
......................................................4分
另一个方面,侧棱![]() 底面
底面![]() ,所以
,所以![]()
而![]() ,所以
,所以![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() ............6分
............6分
(II)解:以点![]() 为原点,射线
为原点,射线![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
则![]() ....................8分
....................8分
设平面![]() 的法向量是
的法向量是![]() ,由
,由![]() 得,..................9分
得,..................9分
![]() ,
,![]() .
.
![]()
所以![]() .....................................................12分
.....................................................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是
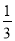 .
.(1)假设
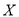 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求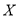 的分布列;
的分布列;(2)设
 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求 的分布列;
的分布列; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
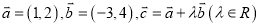 .
.(1)当
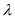 为何值时,
为何值时, 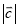 最小? 此时
最小? 此时 与
与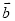 的位置关系如何?
的位置关系如何?(2)当
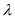 为何值时,
为何值时, 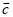 与
与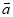 的夹角最小? 此时
的夹角最小? 此时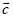 与
与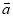 的位置关系如何?
的位置关系如何? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
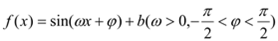 相邻两对称轴间的距离为
相邻两对称轴间的距离为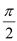 ,若将
,若将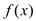 的图像先向左平移
的图像先向左平移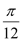 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数 为奇函数.
为奇函数.(1)求
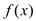 的解析式,并求
的解析式,并求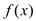 的对称中心;
的对称中心;(2)若关于
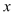 的方程
的方程 在区间
在区间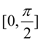 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数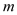 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是
 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是 ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是 .
.(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
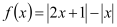 .
.(I)求证:
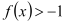 恒成立;
恒成立;(II)若存在实数
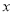 ,使得
,使得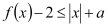 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
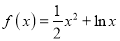 .
.(I)求函数
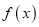 在
在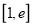 上的最值;
上的最值;(II)已知函数
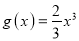 ,求证:
,求证: ,
,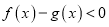 恒成立.
恒成立.
相关试题

