【题目】已知函数 ![]() .
.
(1)求函数y=f(x)的解析式,并用“五点法作图”在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象; 
(2)设α∈(0,π),f( ![]() )=
)= ![]() ,求sinα的值.
,求sinα的值.
参考答案:
【答案】
(1)解:∵ ![]() =
= ![]() ,
,
由 ![]() 知:
知:
x | 0 |
|
| x1,y1 |
| π |
|
|
| π |
| 2π |
|
|
| ﹣1 | 0 | 1 | 0 |
|
故函数y=f(x)在区间[0,π]上图象是

(2)解:法一:∵ ![]() ,
,
∴ ![]() ,
,
![]() ,
,
∵α∈(0,π),
∴sinα>0,
∴ ![]() .
.
法二:∵ ![]() ,
, ![]() ,①
,①
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
又∵α∈(0,π),
∴sinα>0,
∴cos<0,
∴ ![]() ,②
,②
由①②得,∴ ![]()
【解析】(1)利用三角函数恒等变换的应用化简可得函数解析式,根据五点法,求出对应的五点,即可得到结论.(2)法一:由已知可求 ![]() ,利用两角差的正弦函数公式可求sinα的值;法二:由已知可得
,利用两角差的正弦函数公式可求sinα的值;法二:由已知可得 ![]() ,进而可求
,进而可求 ![]() ,联立即可得解.
,联立即可得解.
【考点精析】根据题目的已知条件,利用五点法作函数y=Asin(ωx+φ)的图象的相关知识可以得到问题的答案,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)求f(x)的极值;
(2)当0<x<e时,求证:f(e+x)>f(e﹣x);
(3)设函数f(x)图象与直线y=m的两交点分别为A(x1 , f(x1)、B(x2 , f(x2)),中点横坐标为x0 , 证明:f'(x0)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象与
的图象与 轴交于点
轴交于点 ,周期是
,周期是 .
.(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点
 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
,  时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.(1)求椭圆
 的方程式;
的方程式;(2)已知动直线
 与椭圆
与椭圆 相交于
相交于 两点.
两点.①若线段
 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率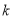 的值;
的值;②已知点
 ,求证:
,求证:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;③线性回归方程
 必过
必过 ;
;④在一个2×2列联表中,由计算得
 =13.079,则有99%的把握确认这两个变量间有关系(其中
=13.079,则有99%的把握确认这两个变量间有关系(其中 );
);其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为
 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为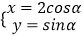 (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为  ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
相关试题

