【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据周期是![]() 可得
可得![]() 的值,再由图象与
的值,再由图象与![]() 轴交于点
轴交于点![]() 求得
求得![]() 的值,从而可得函数解析式,根据余弦函数的性质可求得函数
的值,从而可得函数解析式,根据余弦函数的性质可求得函数![]() 图象的对称轴方程和对称中心;(2)点
图象的对称轴方程和对称中心;(2)点![]()
![]() 是
是![]() 的中点,点
的中点,点![]() ,利用中点坐标公式求出
,利用中点坐标公式求出![]() 的坐标,点
的坐标,点![]() 是该函数图象上一点,代入函数解析式,化简,根据
是该函数图象上一点,代入函数解析式,化简,根据![]() ,求解
,求解![]() 的值.
的值.
试题解析:(1)由题意,周期是π,即![]() .
.
由图象与y轴交于点(0,![]() ),∴
),∴![]() ,可得
,可得![]() ,
,
∵0≤φ≤![]() ,
,![]()
得函数解析式![]() .
.
由![]() ,可得对称轴方程为
,可得对称轴方程为![]() ,(k∈Z)
,(k∈Z)
由![]() ,可得对称中心坐标为(
,可得对称中心坐标为(![]() ,0),(k∈Z)
,0),(k∈Z)
(2)![]() 点Q
点Q![]() 是PA的中点, A
是PA的中点, A![]() ,∴P的坐标为
,∴P的坐标为![]() ,
,
由![]() ,可得P的坐标为
,可得P的坐标为![]() ,
,
又∵点P是该函数图象上一点,
∴![]() ,
,
整理可得:![]() ,
,
∵x0∈![]() ,∴
,∴![]() ,
,
故![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
 中,
中, ,
, ,且
,且 .
.
(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,g(x)=0.5x2﹣bx,(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上不单调,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)﹣k=0只有1个根
(3)设函数g(x)=x2﹣2ax+a,若对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
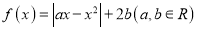 .
.(1)当
 时,解方程
时,解方程 ;
; (2)当
 时,若不等式
时,若不等式 在
在 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;(3)若a为常数,且函数
 在区间
在区间 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
相关试题

