【题目】已知函数 ![]() .
.
(1)求f(x)的极值;
(2)当0<x<e时,求证:f(e+x)>f(e﹣x);
(3)设函数f(x)图象与直线y=m的两交点分别为A(x1 , f(x1)、B(x2 , f(x2)),中点横坐标为x0 , 证明:f'(x0)<0.
参考答案:
【答案】
(1)解:f′(x)= ![]() ,f(x)的定义域是(0,+∞),
,f(x)的定义域是(0,+∞),
x∈(0,e)时,f′(x)>0,f(x)单调递增;
x∈(e,+∞)时,f'(x)<0,f(x)单调递减.
当x=e时,f(x)取极大值为 ![]() ,无极小值
,无极小值
(2)解:要证f(e+x)>f(e﹣x),即证: ![]() ,
,
只需证明:(e﹣x)ln(e+x)>(e+x)ln(e﹣x).
设F(x)=(e﹣x)ln(e+x)﹣(e+x)ln(e﹣x),
![]() ,
,
∴F(x)>F(0)=0,
故(e﹣x)ln(e+x)>(e+x)ln(e﹣x),
即f(e+x)>f(e﹣x)
(3)解:证明:不妨设x1<x2,由(1)知0<x1<e<x2,∴0<e﹣x1<e,
由(2)得f[e+(e﹣x1)]>f[e﹣(e﹣x1)]=f(x1)=f(x2),
又2e﹣x1>e,x2>e,且f(x)在(e,+∞)上单调递减,
∴2e﹣x1<x2,即x1+x2>2e,
∴ ![]() ,∴f'(x0)<0
,∴f'(x0)<0
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的极值即可;(2)问题转化为证明(e﹣x)ln(e+x)>(e+x)ln(e﹣x),设F(x)=(e﹣x)ln(e+x)﹣(e+x)ln(e﹣x),根据函数的单调性证明即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,且a2=﹣14,a5=﹣5.
(1)求数列{an}的通项an;
(2)求{an}前n项和Sn的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,其中向量
,其中向量  (x∈R),
(x∈R),
(1)求函数y=f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为a、b、c,已知f (A)=2,a= ,b=
,b=  ,求边长c的值.
,求边长c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象与
的图象与 轴交于点
轴交于点 ,周期是
,周期是 .
.(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点
 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
,  时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.(1)求椭圆
 的方程式;
的方程式;(2)已知动直线
 与椭圆
与椭圆 相交于
相交于 两点.
两点.①若线段
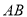 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率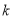 的值;
的值;②已知点
 ,求证:
,求证:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)求函数y=f(x)的解析式,并用“五点法作图”在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象;
(2)设α∈(0,π),f( )=
)=  ,求sinα的值.
,求sinα的值.
相关试题

