【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
参考答案:
【答案】
(1)解:曲线C1的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,
可得直角坐标方程: ![]() .
.
直线l的参数方程为 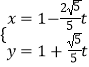 (t为参数),
(t为参数),
消去参数t可得普通方程:x+2y﹣3=0
(2)解: ![]() ,直角坐标为(2,2),
,直角坐标为(2,2), ![]() ,
,
∴M到l的距离 ![]() ≤
≤ ![]() ,
,
从而最大值为 ![]()
【解析】(1)曲线C1的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,可得直角坐标方程.直线l的参数方程为 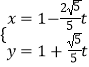 (t为参数),消去参数t可得普通方程.(2)
(t为参数),消去参数t可得普通方程.(2) ![]() ,直角坐标为(2,2),
,直角坐标为(2,2), ![]() ,利用点到直线的距离公式及其三角函数的单调性可得最大值.
,利用点到直线的距离公式及其三角函数的单调性可得最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.(1)求椭圆
 的方程式;
的方程式;(2)已知动直线
 与椭圆
与椭圆 相交于
相交于 两点.
两点.①若线段
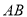 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率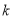 的值;
的值;②已知点
 ,求证:
,求证:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)求函数y=f(x)的解析式,并用“五点法作图”在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象;
(2)设α∈(0,π),f( )=
)=  ,求sinα的值.
,求sinα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;③线性回归方程
 必过
必过 ;
;④在一个2×2列联表中,由计算得
 =13.079,则有99%的把握确认这两个变量间有关系(其中
=13.079,则有99%的把握确认这两个变量间有关系(其中 );
);其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】收入是衡量一个地区经济发展水平的重要标志之一,影响收入的因素有很多,为分析学历对收入的作用,某地区调查机构欲对本地区进行了此项调查.

(1)你认为应采用何种抽样方法进行调查?
(2)经调查得到本科学历月均收入条形图如图,试估算本科学历月均收入
 的值?
的值?(3)设学年为
 ,令
,令 ,月均收入为
,月均收入为 ,已知调查机构调查结果如下表
,已知调查机构调查结果如下表学历 (年)
小学
初中
高中
本科
硕士生
博士生

6
9
12
16
19
22

2.0
2.7
3.7
5.8
7.8

2210
2410
2910

6960
从散点图中可看出
 和
和 的关系可以近似看成是一次函数图像. 若回归直线方程为
的关系可以近似看成是一次函数图像. 若回归直线方程为 ,试预测博士生的平均月收入.
,试预测博士生的平均月收入. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线的顶点与焦点分别是椭圆
 的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

