【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
参考答案:
【答案】
(1)解:法一:f(x)=|x+a|+|2x﹣b|=|x+a|+|x﹣ ![]() |+|x﹣
|+|x﹣ ![]() |,
|,
∵|x+a|+|x﹣ ![]() |≥|(x+a)﹣(x﹣
|≥|(x+a)﹣(x﹣ ![]() )|=a+
)|=a+ ![]() 且|x﹣
且|x﹣ ![]() |≥0,
|≥0,
∴f(x)≥a+ ![]() ,当x=
,当x= ![]() 时取等号,即f(x)的最小值为a+
时取等号,即f(x)的最小值为a+ ![]() ,
,
∴a+ ![]() =1,2a+b=2;
=1,2a+b=2;
法二:∵﹣a< ![]() ,∴f(x)=|x+a|+|2x﹣b|=
,∴f(x)=|x+a|+|2x﹣b|= 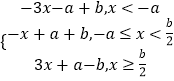 ,
,
显然f(x)在(﹣∞, ![]() ]上单调递减,f(x)在[
]上单调递减,f(x)在[ ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f(x)的最小值为f( ![]() )=a+
)=a+ ![]() ,
,
∴a+ ![]() =1,2a+b=2
=1,2a+b=2
(2)解:方法一:∵a+2b≥tab恒成立,∴ ![]() ≥t恒成立,
≥t恒成立,
![]() =
= ![]() +
+ ![]() =(
=( ![]() +
+ ![]() )(2a+b )
)(2a+b ) ![]() =
= ![]() (1+4+
(1+4+ ![]() +
+ ![]() )
) ![]() ,
,
当a=b= ![]() 时,
时, ![]() 取得最小值
取得最小值 ![]() ,
,
∴ ![]() ≥t,即实数t的最大值为
≥t,即实数t的最大值为 ![]() ;
;
方法二:∵a+2b≥tab恒成立,
∴ ![]() ≥t恒成立,
≥t恒成立,
t≤ ![]() =
= ![]() +
+ ![]() 恒成立,
恒成立,
![]() +
+ ![]() =
= ![]() +
+ ![]() ≥
≥ ![]() =
= ![]() ,
,
∴ ![]() ≥t,即实数t的最大值为
≥t,即实数t的最大值为 ![]() ;
;
方法三:∵a+2b≥tab恒成立,
∴a+2(2﹣a)≥ta(2﹣a)恒成立,
∴2ta2﹣(3+2t)a+4≥0恒成立,
∴(3+2t)2﹣326≤0,
∴ ![]() ≤t≤
≤t≤ ![]() ,实数t的最大值为
,实数t的最大值为 ![]()
【解析】(1)法一:根据绝对值的性质求出f(x)的最小值,得到x= ![]() 时取等号,证明结论即可;法二:根据f(x)的分段函数的形式,求出f(x)的最小值,证明即可;(2)法一,二:问题转化为
时取等号,证明结论即可;法二:根据f(x)的分段函数的形式,求出f(x)的最小值,证明即可;(2)法一,二:问题转化为 ![]() ≥t恒成立,根据基本不等式的性质求出
≥t恒成立,根据基本不等式的性质求出 ![]() 的最小值,从而求出t的范围即可;法三:根据二次函数的性质判断即可.
的最小值,从而求出t的范围即可;法三:根据二次函数的性质判断即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)>ex的解集为( )
A.(﹣∞,0)
B.(0,+∞)
C.(1,+∞)
D.(4,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为
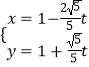 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为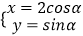 (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为  ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx在x=﹣
 与x=1处都取得极值.
与x=1处都取得极值.
(1)求a,b的值;
(2)求曲线y=f(x)在x=2处的切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为
 ,每次考B科合格的概率均为
,每次考B科合格的概率均为  .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(I)求甲恰好3次考试通过的概率;
(II)记甲参加考试的次数为ξ,求ξ的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 数列
数列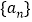 的前
的前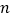 项和,对任意
项和,对任意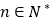 ,都有
,都有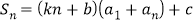 (
(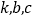 为常数).
为常数).(1)当
 时,求
时,求 ;
;(2)当
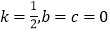 时,
时,(ⅰ)求证:数列
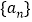 是等差数列;
是等差数列;(ⅱ)若对任意
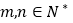 ,必存在
,必存在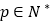 使得
使得 ,已知
,已知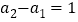 ,且
,且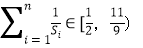 ,
,求数列
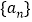 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( )
A.9
B.15
C.18
D.30
相关试题

