【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
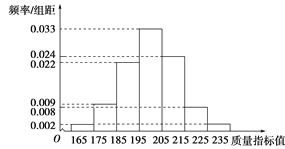
(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附: ![]() ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
参考答案:
【答案】(1)150(2)(ⅰ) 0.6826. (ⅱ) 68.26.
【解析】试题分析:
(1)利用题中所给的数据可得平均数![]() ,方差
,方差![]() ;
;
(2)利用正态分布的对称性可得:P(187.8<Z<212.2)=0.6826.
(3)利用(i)的结论结合题意可得![]() .
.
试题解析:
(1)抽取产品的质量指标值的样本平均数x-和样本方差s2分别为
![]() =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(2)(ⅰ)由(1)知,Z~N(200,150),从而
P(187.8<Z<212.2)=P(200-12.2<Z<200+12.2)=0.6826.
(ⅱ)由(ⅰ)知,一件产品的质量指标值位于区间(187.8,212.2)的概率为0.682 6,依题意知X~B(100,0.6826),所以E(X)=100×0.682 6=68.26.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为
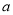 ,视力在4.6到5.0之间的学生数
,视力在4.6到5.0之间的学生数 ,
, 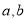 的值分别为( )
的值分别为( )
A.
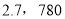 B.
B. 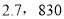 C.
C. 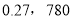 D.
D. 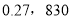
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
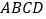 为直角梯形,
为直角梯形,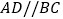 ,
,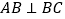 ,
,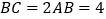 ,
,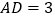 ,
,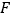 为
为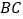 中点,
中点,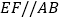 ,
,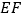 与
与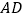 交于点
交于点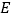 ,沿
,沿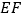 将四边形
将四边形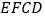 折起,连接
折起,连接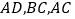 .
.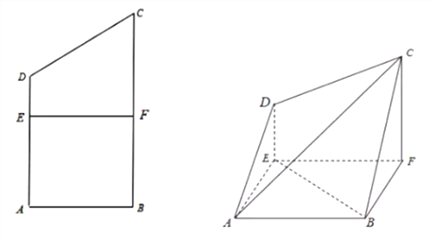
(1)求证:
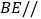 平面
平面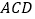 ;
; (2)若平面
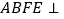 平面
平面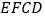 .
.(I)求二面角
 的平面角的大小;
的平面角的大小;(II)线段
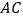 上是否存在点
上是否存在点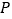 ,使
,使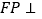 平面
平面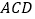 ,若存在,求出
,若存在,求出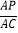 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电子元件厂对一批新产品的使用寿命进行检验,并且厂家规定使用寿命在
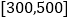 为合格品,使用寿命超过500小时为优质品,质检科抽取了一部分产品做样本,经检测统计后,绘制出了该产品使用寿命的频率分布直方图(如图):
为合格品,使用寿命超过500小时为优质品,质检科抽取了一部分产品做样本,经检测统计后,绘制出了该产品使用寿命的频率分布直方图(如图):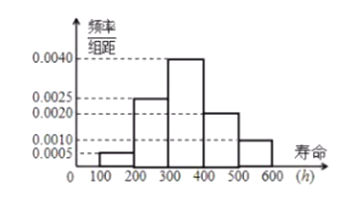
(1)根据频率分布直方图估计该厂产品为合格品或优质品的概率,并估计该批产品的平均使用寿命;
(2)从这批产品中,采取随机抽样的方法每次抽取一件产品,抽取4次,若以上述频率作为概率,记随机变量
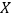 为抽出的优质品的个数,列出
为抽出的优质品的个数,列出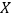 的分布列,并求出其数学期望.
的分布列,并求出其数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届广西陆川县中学高三文上学期二模】已知函数
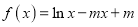 .
.(I)求函数
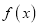 的单调区间;
的单调区间;(II)若
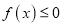 在
在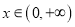 上恒成立,求实数
上恒成立,求实数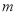 的取值范围;
的取值范围;(III)在(II)的条件下,对任意的
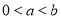 ,求证:
,求证: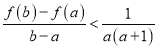 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为
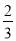 ,答对文科题的概率均为
,答对文科题的概率均为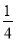 ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分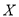 的分布列与数学期望
的分布列与数学期望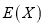 .
.
相关试题

