【题目】【2017届广西陆川县中学高三文上学期二模】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证: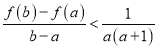 .
.
参考答案:
【答案】(I)当![]() 时,
时,![]() 在
在![]() 上单调递增,无单调递减区间,当
上单调递增,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】
试题分析:(I)利用![]() 时
时![]() 为单调增函数,
为单调增函数,![]() 时
时![]() 为单调减函数这一性质来分情况讨论题中
为单调减函数这一性质来分情况讨论题中![]() 单调区间问题;(II)根据函数单调性与最值,若
单调区间问题;(II)根据函数单调性与最值,若![]() 在
在![]() 上恒成立,则函数的最大值小于或等于零.当
上恒成立,则函数的最大值小于或等于零.当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,说明
,说明![]() 时
时![]() ,不合题意舍去.当
,不合题意舍去.当![]() 时,
时,![]() 的最大值小于零.但
的最大值小于零.但![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 只能等于零.令
只能等于零.令![]() 即可求得答案;(III)首先将
即可求得答案;(III)首先将![]() 的表达式表达出来,化简转化为
的表达式表达出来,化简转化为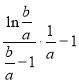 的形式,再根据(II)的结论得到
的形式,再根据(II)的结论得到![]() ,后逐步化简
,后逐步化简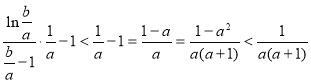 ,原命题得证.
,原命题得证.
试题解析:(I)![]() ,
,
当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上单调递增,无单调递减区间;
上单调递增,无单调递减区间;
当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() ,此时
,此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)由(I)知:当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() ,显然不成立;
,显然不成立;
当![]() 时,
时,![]() ,只需
,只需![]() 即可,
即可,
令![]() ,则
,则![]() ,
,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() .
.
![]() 对
对![]() 恒成立,也就是
恒成立,也就是![]() 对
对![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,![]() 若
若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() .
.
(III)证明: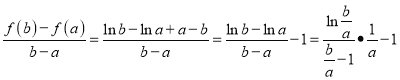 ,
,
由(II)得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又由![]() 得
得![]() ,所以有
,所以有![]() ,即
,即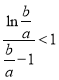 .
.
则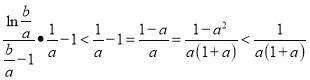 ,
,
则原不等式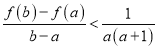 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子元件厂对一批新产品的使用寿命进行检验,并且厂家规定使用寿命在
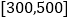 为合格品,使用寿命超过500小时为优质品,质检科抽取了一部分产品做样本,经检测统计后,绘制出了该产品使用寿命的频率分布直方图(如图):
为合格品,使用寿命超过500小时为优质品,质检科抽取了一部分产品做样本,经检测统计后,绘制出了该产品使用寿命的频率分布直方图(如图):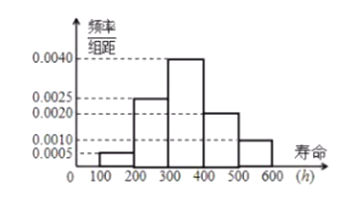
(1)根据频率分布直方图估计该厂产品为合格品或优质品的概率,并估计该批产品的平均使用寿命;
(2)从这批产品中,采取随机抽样的方法每次抽取一件产品,抽取4次,若以上述频率作为概率,记随机变量
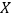 为抽出的优质品的个数,列出
为抽出的优质品的个数,列出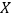 的分布列,并求出其数学期望.
的分布列,并求出其数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
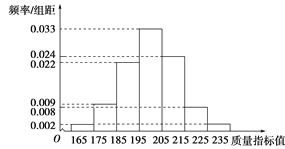
(1)求这500件产品质量指标值的样本平均数
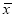 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数
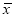 ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附:
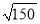 ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为
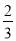 ,答对文科题的概率均为
,答对文科题的概率均为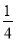 ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分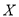 的分布列与数学期望
的分布列与数学期望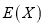 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
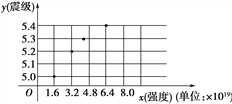
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图(如图)可知a的值等于________.(取lg 2=0.3进行计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥
 的直观图和三视图如下:
的直观图和三视图如下: (1)求证:
 底面
底面 ;
;(2)求三棱锥
 的体积;
的体积;(3)求三棱锥
 的侧面积.
的侧面积.

相关试题

