【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若点
.若点![]() 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)先明确函数定义域,再求函数导数![]() ,根据导函数零点进行分类讨论:当
,根据导函数零点进行分类讨论:当![]() 时,
时, ![]() ,因此减区间为
,因此减区间为![]() ,当
,当![]() 时,
时, ![]() 递增区间为
递增区间为![]() ,递减区间为
,递减区间为![]() (Ⅱ)根据导数几何意义得切线的斜率
(Ⅱ)根据导数几何意义得切线的斜率![]() ,再根据点斜式写出切线方程
,再根据点斜式写出切线方程![]() ,得点
,得点![]() 的纵坐标
的纵坐标![]() ,即不等式
,即不等式![]() 恒成立,而不等式恒成立问题,一般转化为对应函数最值问题::
恒成立,而不等式恒成立问题,一般转化为对应函数最值问题:: ![]() 的最大值,利用导数研究函数
的最大值,利用导数研究函数![]() 单调性,为单调递减,再利用洛必达法则得
单调性,为单调递减,再利用洛必达法则得![]() ,因此
,因此![]() ,也可直接构造差函数,分类讨论最值进行求解
,也可直接构造差函数,分类讨论最值进行求解
试题解析:解:(1)当![]() 时,
时, ![]() .……………………1分
.……………………1分
所以,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .………………3分
.………………3分
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .……………………4分
.……………………4分
(2)因为![]() ,所以
,所以![]() 处切线的斜率
处切线的斜率![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,
,
令![]() 得,
得, ![]() .………………………………5分
.………………………………5分
当![]() 时,要使得点
时,要使得点![]() 的纵坐标恒小于1,
的纵坐标恒小于1,
只需![]() ,即
,即![]() .…………………………6分
.…………………………6分
令![]() ,则
,则![]() .………………………………7分
.………………………………7分
因为![]() ,所以
,所以![]() ,
,
①若![]() ,即
,即![]() 时,
时, ![]() ,
,
所以,当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 恒成立,所以
恒成立,所以![]() 满足题意.………………………………8分
满足题意.………………………………8分
②若![]() 即
即![]() 时,
时, ![]() ,
,
所以,当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() 不满足题意.…………………………9分
不满足题意.…………………………9分
③若![]() ,即
,即![]() 时,
时, ![]() ,
,
则![]() 、
、![]() 、
、![]() 的关系如下表:
的关系如下表:
|
|
|
|
|
| 0 |
|
| 递减 | 极小值 | 递增 |
所以![]() ,所以
,所以![]() 不满足题意,
不满足题意,
结合①②③,可得,当![]() 时,
时, ![]() 时,此时点
时,此时点![]() 的纵坐标恒小于1.………………12分
的纵坐标恒小于1.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且f(x)满足f(x+π)=f(x),当[0,
 )时,f(x)=tanx,则f(
)时,f(x)=tanx,则f(  )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y﹣3=0平行,求a的值;
(2)若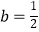 ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意角α的终边经过点P(﹣3,m),且cosα=﹣
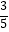
(1)求m的值.
(2)求sinα与tanα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:f(x)=
 在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
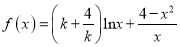 ,其中常数
,其中常数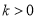 .
.(Ⅰ)讨论
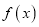 在
在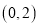 上的单调性;
上的单调性;(Ⅱ)当
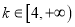 时,若曲线
时,若曲线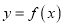 上总存在相异两点
上总存在相异两点 ,使曲线
,使曲线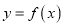 在
在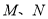 两点处的切线互相平行,试求
两点处的切线互相平行,试求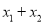 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )
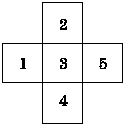
A.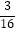
B.
C.
D.
相关试题

