【题目】已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y﹣3=0平行,求a的值;
(2)若 ![]() ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.
参考答案:
【答案】
(1)
解:函数f(x)的定义域为 ![]() .
. ![]()
由题意 ![]() ,解得
,解得 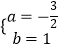 ∴
∴ ![]() .
.
(2)
解:若 ![]() ,则
,则 ![]() .
. ![]() .
.
(1)令 ![]() ,由函数定义域可知,4x+2>0,所以2x+4a+1>0
,由函数定义域可知,4x+2>0,所以2x+4a+1>0
①当a≥0时, ![]() ,f'(x)>0,函数f(x)单调递增;
,f'(x)>0,函数f(x)单调递增;
②当a<0时, ![]() ,f'(x)>0,函数f(x)单调递增;
,f'(x)>0,函数f(x)单调递增;
(2)令 ![]() ,即2x+4a+1<0
,即2x+4a+1<0
①当a≥0时,不等式f'(x)<0无解;
②当a<0时, ![]() ,f'(x)<0,函数f(x)单调递减;
,f'(x)<0,函数f(x)单调递减;
综上:当a≥0时,函数f(x)在区间 ![]() 为增函数;
为增函数;
当a<0时,函数f(x)在区间 ![]() 为增函数;
为增函数;
在区间 ![]() 为减函数.
为减函数.
【解析】(1)先求函数的定义域,然后求出函数的导函数,根据导数的几何意义和极值的定义建立方程组 ![]() ,解之即可;(2)讨论a的正负,然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间.
,解之即可;(2)讨论a的正负,然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=f(x)的定义域为D,若对于任意x1、x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx﹣3的某一个对称中心,并利用对称中心的上述定义,可得到f(
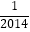 )+f(
)+f( 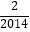 )+…+f(
)+…+f( 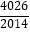 )+f(
)+f( 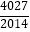 )的值为( )
)的值为( )
A.4027
B.﹣4027
C.8054
D.﹣8054 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程:
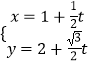 (t为参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,曲线C的极坐标方程为ρ2=
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,曲线C的极坐标方程为ρ2= 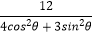 .
.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设曲线C与直线l交于A,B两点,若P(1,2),求|PA|+|PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且f(x)满足f(x+π)=f(x),当[0,
 )时,f(x)=tanx,则f(
)时,f(x)=tanx,则f(  )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意角α的终边经过点P(﹣3,m),且cosα=﹣
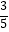
(1)求m的值.
(2)求sinα与tanα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求
时,求 的单调区间;
的单调区间;(Ⅱ)设函数
 在点
在点 处的切线为
处的切线为 ,直线
,直线 与
与 轴相交于点
轴相交于点 .若点
.若点 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:f(x)=
 在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
相关试题

