【题目】如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )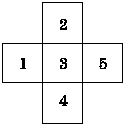
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:由题意可知小青蛙三次跳动后的所有情况有:
(3→1→3→1),(3→1→3→2),(3→1→3→4),(3→1→3→5);
(3→2→3→2),(3→2→3→1),(3→2→3→4),(3→2→3→5),
(3→4→3→4),(3→4→3→1),(3→4→3→2),(3→4→3→5),
(3→5→3→5),(3→5→3→1),(3→5→3→2),(3→5→3→4).
共有16种,
满足题意的有:(3→1→3→5),(3→2→3→5),(3→4→3→5)有3种.
由古典概型的概率的计算公式可得:
青蛙在第三次跳动后,首次进入5处的概率是: ![]() .
.
故选:A.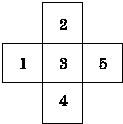
列出小青蛙三次跳动后的所有情况,找出满足题意的可能数目,然后利用古典概型概率公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求
时,求 的单调区间;
的单调区间;(Ⅱ)设函数
 在点
在点 处的切线为
处的切线为 ,直线
,直线 与
与 轴相交于点
轴相交于点 .若点
.若点 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:f(x)=
 在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
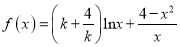 ,其中常数
,其中常数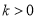 .
.(Ⅰ)讨论
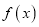 在
在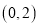 上的单调性;
上的单调性;(Ⅱ)当
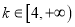 时,若曲线
时,若曲线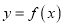 上总存在相异两点
上总存在相异两点 ,使曲线
,使曲线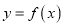 在
在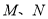 两点处的切线互相平行,试求
两点处的切线互相平行,试求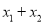 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
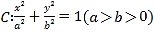 :
: 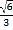 (
(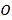 )的离心率为
)的离心率为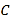 ,以原点
,以原点 为圆心,椭圆
为圆心,椭圆 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线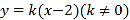 相切.
相切.(Ⅰ)求椭圆
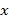 的标准方程;
的标准方程;(Ⅱ)已知点
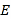 为动直线
为动直线 与椭圆
与椭圆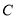 的两个交点,问:在
的两个交点,问:在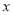 轴上是否存在定点
轴上是否存在定点 ,使得
,使得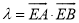 为定值?若存在,试求出点
为定值?若存在,试求出点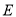 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)在定义域[﹣1,1]是奇函数,当x∈[﹣1,0]时,f(x)=﹣3x2 .
(1)当x∈[0,1],求f(x);
(2)对任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
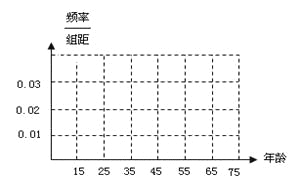
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
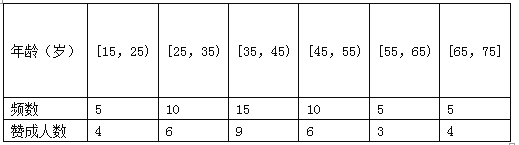
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为
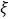 ,求随机变量
,求随机变量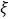 的分布列和数学期望.
的分布列和数学期望.
相关试题

