【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 上总存在相异两点
上总存在相异两点![]() ,使曲线
,使曲线![]() 在
在![]() 两点处的切线互相平行,试求
两点处的切线互相平行,试求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)求导数,对![]() 分类讨论,利用导数的正负,即可得到
分类讨论,利用导数的正负,即可得到![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)利用过![]() 两点处的切线互相平行,建立方程,结合基本不等式,再求最值,即可求解
两点处的切线互相平行,建立方程,结合基本不等式,再求最值,即可求解![]() 的取值范围。
的取值范围。
试题解析:(Ⅰ)由已知得, ![]() 的定义域为
的定义域为![]() ,且
,且
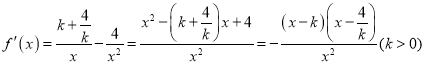 ,
,
①当![]() 时,
时, ![]() ,且
,且![]() ,
,
所以![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
所以,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
②当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() 在
在![]() 上是减函数;
上是减函数;
③当![]() 时,
时, ![]() ,
,
所以![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
所以函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(Ⅱ)由题意,可得![]() ,
, ![]() 且
且![]()
即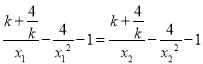 ,化简得,
,化简得, ![]()
由![]() ,得
,得![]()
即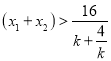 对
对![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 对
对![]() 恒成立
恒成立
∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,所以
,所以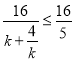 ,
,
所以![]() ,
,
故![]() 取值范围为
取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意角α的终边经过点P(﹣3,m),且cosα=﹣
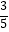
(1)求m的值.
(2)求sinα与tanα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求
时,求 的单调区间;
的单调区间;(Ⅱ)设函数
 在点
在点 处的切线为
处的切线为 ,直线
,直线 与
与 轴相交于点
轴相交于点 .若点
.若点 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:f(x)=
 在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q;x1x2是方程x2﹣ax﹣2=0的两个实根,不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1,1]恒成立;若¬p∧q为真,试求实数m的取值范围. -
科目: 来源: 题型:
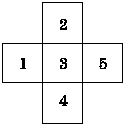
查看答案和解析>>【题目】如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )
A.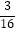
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
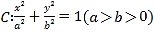 :
: 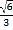 (
( )的离心率为
)的离心率为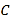 ,以原点
,以原点 为圆心,椭圆
为圆心,椭圆 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线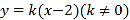 相切.
相切.(Ⅰ)求椭圆
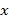 的标准方程;
的标准方程;(Ⅱ)已知点
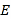 为动直线
为动直线 与椭圆
与椭圆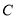 的两个交点,问:在
的两个交点,问:在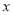 轴上是否存在定点
轴上是否存在定点 ,使得
,使得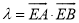 为定值?若存在,试求出点
为定值?若存在,试求出点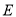 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)在定义域[﹣1,1]是奇函数,当x∈[﹣1,0]时,f(x)=﹣3x2 .
(1)当x∈[0,1],求f(x);
(2)对任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范围.
相关试题

