【题目】[选修4-5:不等式选讲]
已知函数![]() .
.
(1)解不等式:![]() ;
;
(2)对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)解法一:写出分段函数![]() 的解析式,讨论
的解析式,讨论![]() 的范围,求出分段函数不同自变量范围的不等式的解,再求这些解的并集即可.
的范围,求出分段函数不同自变量范围的不等式的解,再求这些解的并集即可.
解法二:写出分段函数![]() 的解析式,绘制函数图象,计算函数
的解析式,绘制函数图象,计算函数![]() 与
与![]() 的交点坐标,根据函数图象确定不等式的解.
的交点坐标,根据函数图象确定不等式的解.
解法三:根据绝对值在数轴上的几何意义,确定不等式的解.
(2)将![]() 恒成立问题转化成
恒成立问题转化成![]() 问题,确定
问题,确定![]() 后,解关于
后,解关于![]() 的一元二次不等式,即可求出实数
的一元二次不等式,即可求出实数![]() 的取值范围.
的取值范围.
解法一:根据三角不等式,确定函数最小值
解法二:根据函数图象,确定函数最小值.
详解:(1)解法一: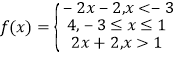
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
所以不等式![]() 的解集为
的解集为![]() ;
;
(1)解法二:
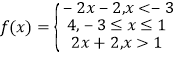 ,两个函数的图象如图所示:
,两个函数的图象如图所示:
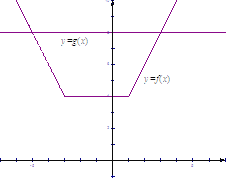
由图像可知,两函数图象的交点为
![]() 和
和![]() ,
,
所以不等式![]() 即
即![]() 的解集为
的解集为![]()
(注:如果作出函数![]() 的图象,写出
的图象,写出![]() 的解集,可参照解法2的标准给分)
的解集,可参照解法2的标准给分)
解法三:如图,

设数轴上与![]() 对应的点分别是
对应的点分别是![]() ,那么
,那么![]() 两点的距离是4,因此区间
两点的距离是4,因此区间![]() 上的数都是原不等式的解。
上的数都是原不等式的解。
先在数轴上找出与点![]() 的距离之和为
的距离之和为![]() 的点,将点
的点,将点![]() 向左移动2个单位到点
向左移动2个单位到点![]() ,这时有
,这时有![]() ,
,
同理,将点![]() 向右移动2个单位到点
向右移动2个单位到点![]() ,这时也有
,这时也有![]() ,
,
从数轴上可以看到,点![]() 与
与![]() 之间的任何点到点
之间的任何点到点![]() 的距离之和都小于8, 点
的距离之和都小于8, 点![]() 的左边或点
的左边或点![]() 的右边的任何点到点
的右边的任何点到点![]() 的距离之和都大于8,
的距离之和都大于8,
所以,原不等式的解集是![]()
(2)解法一:![]() ,
,
当![]() 时“
时“![]() ”成立,
”成立,
又![]() 任意
任意![]() ,
,![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
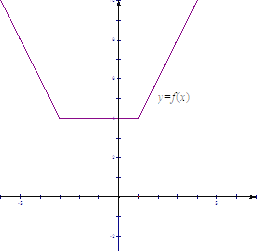
解法二: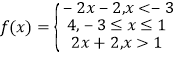
作函数![]() 的图象如图:
的图象如图:
由图象可知,函数![]() 的最小值为4,
的最小值为4,
(注:如果第(1)问用解法2,可直接由(1)得最小值为4,不必重复说明)
又![]() 任意
任意![]() ,
,![]() 恒成立,
恒成立,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】手机支付也称为移动支付
 ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.组数
第l组
第2组
第3组
第4组
第5组
分组





频数
20
36
30
10
4

(1)求
 ;
;(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价
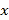 (元)
(元)8
8.2
8.4
8.6
8.8
9
销量
 (件)
(件)90
84
83
80
75
68
(1)求销量
 (件)关于单价
(件)关于单价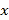 (元)的线性回归方程
(元)的线性回归方程 ;
;(2)若单价定为10元,估计销量为多少件;
(3)根据销量
 关于单价
关于单价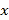 的线性回归方程,要使利润
的线性回归方程,要使利润 最大,应将价格定为多少?
最大,应将价格定为多少?参考公式:
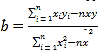 ,
, .参考数据:
.参考数据: ,
,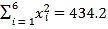
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
-
科目: 来源: 题型:
查看答案和解析>>【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 都是从集合
都是从集合 中任取的一个数,求函数
中任取的一个数,求函数 有零点的概率;
有零点的概率;(2)若
 都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市大约有800万网络购物者,某电子商务公司对该市n名网络购物者某年度上半年的消费情况进行了统计,发现消费金额(单位:万元)都在区间[0.5,1.1]内,其频率分布直方图如图所示.

(1)求该市n名网络购物者该年度上半年的消费金额的平均数与中位数(以各区间的中点值代表该区间的均值).
(2)现从前4组中选取18人进行网络购物爱好调查.
(i)求在前4组中各组应该选取的人数;
(ii)在前2组所选取的人中,再随机选2人,求这2人都是来自第二组的概率.
相关试题

