【题目】已知某市大约有800万网络购物者,某电子商务公司对该市n名网络购物者某年度上半年的消费情况进行了统计,发现消费金额(单位:万元)都在区间[0.5,1.1]内,其频率分布直方图如图所示.

(1)求该市n名网络购物者该年度上半年的消费金额的平均数与中位数(以各区间的中点值代表该区间的均值).
(2)现从前4组中选取18人进行网络购物爱好调查.
(i)求在前4组中各组应该选取的人数;
(ii)在前2组所选取的人中,再随机选2人,求这2人都是来自第二组的概率.
参考答案:
【答案】(1)0.752,0.76;(2)(i)3,4,5,6人;(ii)![]() .
.
【解析】
(1)通过频率分布直方图估计总体的平均值和中位数等数字特征,依照规则即可算出;(2)(i)由分层抽样的特点,即可求出;(ii)利用古典概型计算公式算出即可。
(1)依题意,平均数为![]() =0.55×0.15+0.65×0.2+0.75×0.25+0.85×0.3+0.95×0.08+×1.05×0.02=0.752;
=0.55×0.15+0.65×0.2+0.75×0.25+0.85×0.3+0.95×0.08+×1.05×0.02=0.752;
1.5×0.1+2.0×0.1=0.35<0.5,而1.5×0.1+2.0×0.1+2.5×0.1=0.6>0.5,所以中位数位于[0.7,0.8)之间,
所以中位数为0.7+![]() =0.76.
=0.76.
(2)(i)前4组的频率分别为:0.15,0.2,0.25,0.3,
所以前四组人数比为:0.15:0.2:0.25:0.3=3:4:5:6,
前4组共抽取18人,所以第一组抽取18×![]() =3人,第二组抽取人数为18×
=3人,第二组抽取人数为18×![]() =4人,第3组抽取人数为18×
=4人,第3组抽取人数为18×![]() =5人,第4组抽取人数为18×
=5人,第4组抽取人数为18×![]() =6人.
=6人.
所以前4组中各组应该选取的人数分别为3,4,5,6人.
(ii)由(i)知,第一组抽到3人,第二组抽到4人,
设事件A表示在前2组所选取的人中,再随机选2人,求这2人都是来自第二组,
则P(A)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-5:不等式选讲]
已知函数
 .
.(1)解不等式:
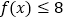 ;
;(2)对任意
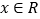 ,
,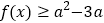 恒成立,求实数
恒成立,求实数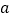 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 都是从集合
都是从集合 中任取的一个数,求函数
中任取的一个数,求函数 有零点的概率;
有零点的概率;(2)若
 都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
年份x
2011
2012
2013
2014
2015
储蓄存款y(千亿元)
5
6
7
8
10
为了研究计算的方便,工作人员将上表的数据进行了处理,
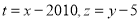 得到表2:
得到表2:时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程
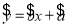 ,
, 其中
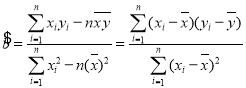 ,
, 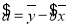 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】据某市供电公司数据,2019年1月份市新能源汽车充电量约270万度,同比2018年增长
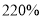 ,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照
,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照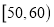 ,
,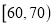 ,…,
,…,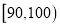 分成5组,制成如图所示的频率分布直方图.
分成5组,制成如图所示的频率分布直方图.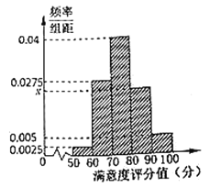
(1)求图中
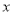 的值并估计样本数据的中位数;
的值并估计样本数据的中位数;(2)已知满意度评分值在
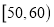 内的男女司机人数比为
内的男女司机人数比为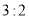 ,从中随机抽取2人进行座谈,求2人均为女司机的概率.
,从中随机抽取2人进行座谈,求2人均为女司机的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且
 .
.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
相关试题

