【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
参考答案:
【答案】(1) ![]() ;(2) 第1组2人,第3组3人,第4组1人;(3)
;(2) 第1组2人,第3组3人,第4组1人;(3) ![]()
【解析】
(1)直接计算![]() .
.
(2)根据分层抽样的规律按照比例抽取.
(3)设第1组抽取的2人为![]() ,
,![]() ,第3组抽取的3人为
,第3组抽取的3人为![]() ,
,![]() ,
,![]() ,第4组抽取的1人为
,第4组抽取的1人为![]() ,排列出所有可能,再计算满足条件的个数,相除得到答案.
,排列出所有可能,再计算满足条件的个数,相除得到答案.
解:(1)由题意可知,
![]() ,
,
(2)第1,3,4组共有60人,所以抽取的比例是![]()
则从第1组抽取的人数为![]() ,从第3组抽取的人数为
,从第3组抽取的人数为![]() ,从第4组抽取的人数为
,从第4组抽取的人数为![]() ;
;
(3)设第1组抽取的2人为![]() ,
,![]() ,第3组抽取的3人为
,第3组抽取的3人为![]() ,
,![]() ,
,![]() ,第4组抽取的1人为
,第4组抽取的1人为![]() ,则从这6人中随机抽取2人有如下种情形:
,则从这6人中随机抽取2人有如下种情形:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共有15个基本事件.
共有15个基本事件.
其中符合“抽取的2人来自同一个组”的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() 共4个基本事件,
共4个基本事件,
所以抽取的2人来自同一个组的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面立角坐标系
 中,过点
中,过点 的圆的圆心
的圆的圆心 在
在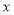 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为 的直线
的直线 相切.
相切.(1)求圆
 的标准方程;
的标准方程;(2)点
 在直线
在直线 上,过点
上,过点 作圆
作圆 的切线
的切线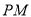 、
、 ,切点分别为
,切点分别为 、
、 ,求经过
,求经过 、
、 、
、 、
、 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(
 元)试销l天,得到如表单价
元)试销l天,得到如表单价 (元)与销量
(元)与销量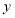 (册)数据:
(册)数据:单价
 (元)
(元)18
19
20
21
22
销量
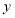 (册)
(册)61
56
50
48
45
(l)根据表中数据,请建立
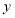 关于
关于 的回归直线方程:
的回归直线方程:(2)预计今后的销售中,销量
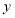 (册)与单价
(册)与单价 (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?附:
 ,
, ,
, ,
,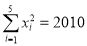 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣lnx+a﹣1,g(x)=
 +ax﹣xlnx,其中a>0.
+ax﹣xlnx,其中a>0.
(1)求f(x)的单调区间;
(2)当x≥1时,g(x)的最小值大于 ﹣lna,求a的取值范围.
﹣lna,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价
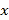 (元)
(元)8
8.2
8.4
8.6
8.8
9
销量
 (件)
(件)90
84
83
80
75
68
(1)求销量
 (件)关于单价
(件)关于单价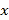 (元)的线性回归方程
(元)的线性回归方程 ;
;(2)若单价定为10元,估计销量为多少件;
(3)根据销量
 关于单价
关于单价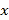 的线性回归方程,要使利润
的线性回归方程,要使利润 最大,应将价格定为多少?
最大,应将价格定为多少?参考公式:
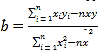 ,
, .参考数据:
.参考数据: ,
,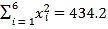
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-5:不等式选讲]
已知函数
 .
.(1)解不等式:
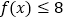 ;
;(2)对任意
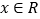 ,
,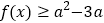 恒成立,求实数
恒成立,求实数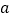 的取值范围.
的取值范围.
相关试题

