【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
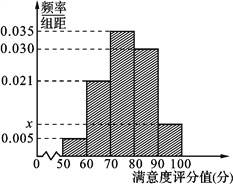
(1) 求图中![]() 的值;
的值;
(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:
(1)利用频率分布直方图的面积为1得到关于![]() 的方程,解方程即可求得实数
的方程,解方程即可求得实数![]() 的值;
的值;
(2)首先确定该分布列为超几何分布,然后写出分布列求解均值即可.
试题解析:
(Ⅰ)由![]() ,解得
,解得![]() .
.
(Ⅱ)满意度评分值在[90,100]内有![]() 人,
人,
其中男生6人,女生3人.
则X的值可以为0,1,2,3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
则X分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以X的期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,椭圆C的参数方程为
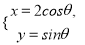 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为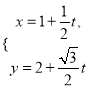 (t为参数).
(t为参数).(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1,C2的极坐标方程分别为ρ=2cosθ,
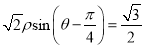 ,射线θ=φ,
,射线θ=φ, 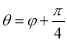 ,
, 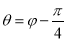 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.(Ⅰ)求证:
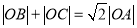 ;
;(Ⅱ)当
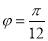 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=xlnx-a(x-1)2-x,g(x)=lnx-2a(x-1),其中常数a∈R.
(Ⅰ)讨论g(x)的单调性;
(Ⅱ)当a>0时,若f(x)有两个零点x1,x2(x1<x2),求证:在区间(1,+∞)上存在f(x)的极值点x0,使得x0lnx0+lnx0-2x0>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线
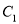 的参数方程是
的参数方程是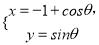 (
(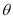 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 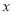 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线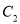 的极坐标方程是
的极坐标方程是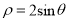 .
.(Ⅰ) 求曲线
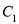 与
与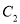 交点的平面直角坐标;
交点的平面直角坐标;(Ⅱ) 点
 分别在曲线
分别在曲线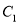 ,
, 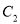 上,当
上,当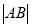 最大时,求
最大时,求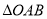 的面积(
的面积( 为坐标原点).
为坐标原点). -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
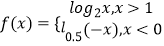 . (I)求
. (I)求 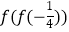 的值;
的值;
(II)若f(a)>f(﹣a),求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x-1|+|2x-1|.
(Ⅰ)若对
 x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=2M.证明:a+b≥2ab.
相关试题

