【题目】在平面直角坐标系xOy中,椭圆C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为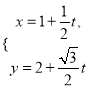 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
参考答案:
【答案】(I) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)利用平方法消去θ得到椭圆C的普通方程为![]() ,根据直线参数方程的几何意义求出直线的斜率,从而可得结果;(Ⅱ)把直线
,根据直线参数方程的几何意义求出直线的斜率,从而可得结果;(Ⅱ)把直线![]() 的方程
的方程 ,代入
,代入![]() 中,利用直线参数方程的几何意义求出直线的斜率结合韦达定理可得结果.
中,利用直线参数方程的几何意义求出直线的斜率结合韦达定理可得结果.
试题解析:(Ⅰ)消去θ得到椭圆C的普通方程为![]() .
.
∵直线![]() 的斜率为
的斜率为![]() ,∴直线l的倾斜角为
,∴直线l的倾斜角为![]() .
.
(Ⅱ)把直线![]() 的方程
的方程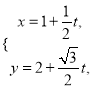 ,代入
,代入![]() 中,
中,
得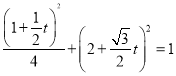 .
.
即![]() ,
,
∴t1·t2=4,即|PA|·|PB|=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={﹣2,3a﹣1,a2﹣3},B={a﹣2,a﹣1,a+1},若A∩B={﹣2},求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
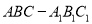 中,底面△ABC是等边三角形,侧面
中,底面△ABC是等边三角形,侧面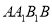 为正方形,且
为正方形,且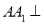 平面ABC,
平面ABC, 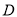 为线段
为线段 上的一点.
上的一点.(Ⅰ) 若
 ∥平面A1CD,确定D的位置,并说明理由;
∥平面A1CD,确定D的位置,并说明理由;(Ⅱ) 在(Ⅰ)的条件下,求二面角
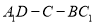 的余弦值.
的余弦值.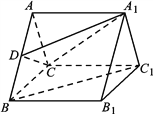
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
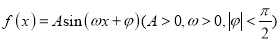 的部分图象如图所示.
的部分图象如图所示.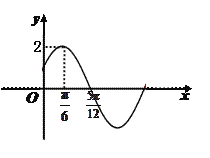
(1) 求函数
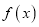 的解析式;
的解析式;(2) 如何由函数
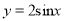 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数 的图象, 写出变换过程;
的图象, 写出变换过程;(3) 若
 ,求
,求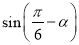 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1,C2的极坐标方程分别为ρ=2cosθ,
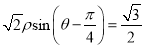 ,射线θ=φ,
,射线θ=φ, 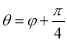 ,
, 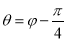 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.(Ⅰ)求证:
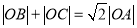 ;
;(Ⅱ)当
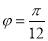 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=xlnx-a(x-1)2-x,g(x)=lnx-2a(x-1),其中常数a∈R.
(Ⅰ)讨论g(x)的单调性;
(Ⅱ)当a>0时,若f(x)有两个零点x1,x2(x1<x2),求证:在区间(1,+∞)上存在f(x)的极值点x0,使得x0lnx0+lnx0-2x0>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
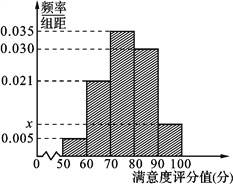
(1) 求图中
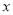 的值;
的值;(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量
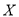 ,求
,求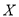 的分布列和数学期望.
的分布列和数学期望.
相关试题

