【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 、
、![]() 在椭圆
在椭圆![]() 上,且四边形
上,且四边形![]() 是矩形,求矩形
是矩形,求矩形![]() 的面积
的面积![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() (2)矩形
(2)矩形![]() 面积
面积![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)由椭圆过点![]() ,且离心率为
,且离心率为![]() ,得到
,得到![]() ,
,![]() ,进而可求出结果;
,进而可求出结果;
(2)先由题意知直线![]() 不垂直于
不垂直于![]() 轴,设直线
轴,设直线![]() ,联立直线与椭圆方程,设
,联立直线与椭圆方程,设![]() ,
,![]() ,根据韦达定理和题中条件可求出
,根据韦达定理和题中条件可求出![]() ;再求出
;再求出![]() 的最大值即可得出结果.
的最大值即可得出结果.
解:(1)因为椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() ,
,
所以![]() ,
,![]() ,又因为
,又因为![]() ,
,
可解得![]() ,
,![]() ,焦距为
,焦距为![]() .
.
所求椭圆的方程为![]() .
.
(2)由题意知直线![]() 不垂直于
不垂直于![]() 轴,可设直线
轴,可设直线![]() ,
,
由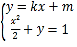 得
得![]() ,
,![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
又因为![]() ,
,![]() ,
,
所以![]()
![]()
![]()
![]()
化简可得![]() .
.
所以![]()
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() .
.
令![]() ,因为
,因为![]()
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
因为矩形![]() 面积
面积![]()
所以矩形![]() 面积
面积![]() 的最大值为
的最大值为![]() .
.
此时直线![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的焦距为
的焦距为 分别为椭圆
分别为椭圆 的左、右顶点,
的左、右顶点, 为椭圆
为椭圆 上的两点(异于
上的两点(异于 ),连结
),连结 ,且
,且 斜率是
斜率是 斜率的
斜率的 倍.
倍.(1)求椭圆
 的方程;
的方程;(2)证明:直线
 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为3的菱形
 中,已知
中,已知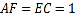 ,且
,且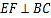 .将梯形
.将梯形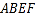 沿直线
沿直线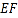 折起,使
折起,使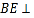 平面
平面 ,如图2,
,如图2,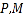 分别是
分别是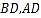 上的点.
上的点.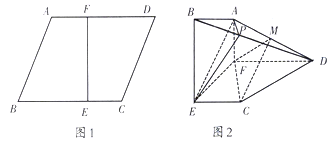
(1)若平面
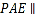 平面
平面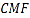 ,求
,求 的长;
的长;(2)是否存在点
 ,使直线
,使直线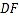 与平面
与平面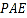 所成的角是
所成的角是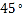 ?若存在,求出
?若存在,求出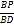 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
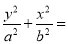 1(a>b>0)经过点(
1(a>b>0)经过点(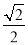 ,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.
,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.(1)求椭圆C的方程
(2)是否存在定点M(异于点F),对任意的动直线l都有kMA+kMB=0,若存在求出点M的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
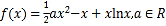 .
.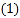 若
若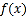 在其定义域上单调递减,求
在其定义域上单调递减,求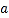 的取值范围;
的取值范围; 若
若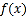 存在两个不同极值点
存在两个不同极值点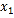 与
与 ,且
,且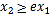 ,求证
,求证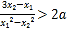 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系
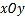 中,直线
中,直线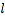 的参数方程为
的参数方程为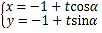 (
(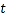 为参数,
为参数,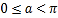 ),以坐标原点
),以坐标原点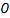 为极点,
为极点,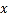 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线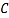 的极坐标方程为
的极坐标方程为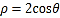 .
.(Ⅰ)若
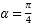 ,求直线
,求直线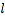 的普通方程及曲线
的普通方程及曲线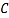 的直角坐标方程;
的直角坐标方程;(Ⅱ)若直线
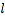 与曲线
与曲线 有两个不同的交点,求
有两个不同的交点,求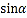 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
相关试题

