【题目】已知函数![]() .
.
![]() 若
若![]() 在其定义域上单调递减,求
在其定义域上单调递减,求![]() 的取值范围;
的取值范围;
![]() 若
若![]() 存在两个不同极值点
存在两个不同极值点![]() 与
与![]() ,且
,且![]() ,求证
,求证![]() .
.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
![]() 先对函数求导,由
先对函数求导,由![]() 在其定义域上单调递减,得到
在其定义域上单调递减,得到![]() 恒成立,即
恒成立,即![]() 恒成立,用导数的方法求出
恒成立,用导数的方法求出![]() 的最小值即可;
的最小值即可;
(2)若![]() 存在两个不同极值点
存在两个不同极值点![]() 与
与![]() ,且
,且![]() ,欲证:
,欲证:![]() ,只需证:
,只需证:![]() ,即证
,即证![]() ,再根据
,再根据![]() ,
,![]() 得到
得到![]() ,
,![]() ,再令
,再令![]() ,得到
,得到![]() ,设
,设![]() ,由导数方法研究其单调性即可得出结论.
,由导数方法研究其单调性即可得出结论.
解:(1)由于![]() 的定义域为
的定义域为![]() ,且
,且![]() ,若在其定义域上单调递减,则
,若在其定义域上单调递减,则![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,
,![]()
则随着![]() 的变化,
的变化,![]() 与
与![]() 的变化如下表所示
的变化如下表所示
|
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以![]() .
.
所以![]()
(2)若![]() 存在两个不同极值点
存在两个不同极值点![]() 与
与![]() ,且
,且![]() ,
,
欲证:![]() .
.
只需证:![]() .
.
只需证:![]() .
.
只需证:![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以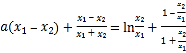
令![]() ,则
,则![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
可知函数![]() 在
在![]() 上单调递增
上单调递增
所以![]()
![]() .
.
所以![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为3的菱形
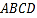 中,已知
中,已知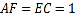 ,且
,且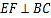 .将梯形
.将梯形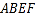 沿直线
沿直线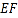 折起,使
折起,使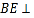 平面
平面 ,如图2,
,如图2,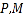 分别是
分别是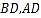 上的点.
上的点.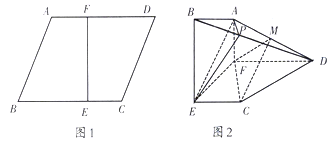
(1)若平面
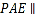 平面
平面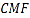 ,求
,求 的长;
的长;(2)是否存在点
 ,使直线
,使直线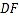 与平面
与平面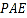 所成的角是
所成的角是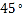 ?若存在,求出
?若存在,求出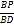 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
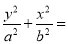 1(a>b>0)经过点(
1(a>b>0)经过点(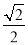 ,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.
,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.(1)求椭圆C的方程
(2)是否存在定点M(异于点F),对任意的动直线l都有kMA+kMB=0,若存在求出点M的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
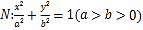 经过点
经过点 ,且离心率为
,且离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)若点
 、
、 在椭圆
在椭圆 上,且四边形
上,且四边形 是矩形,求矩形
是矩形,求矩形 的面积
的面积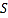 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系
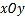 中,直线
中,直线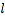 的参数方程为
的参数方程为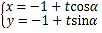 (
(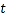 为参数,
为参数,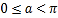 ),以坐标原点
),以坐标原点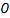 为极点,
为极点,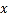 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线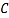 的极坐标方程为
的极坐标方程为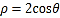 .
.(Ⅰ)若
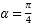 ,求直线
,求直线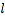 的普通方程及曲线
的普通方程及曲线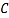 的直角坐标方程;
的直角坐标方程;(Ⅱ)若直线
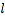 与曲线
与曲线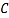 有两个不同的交点,求
有两个不同的交点,求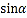 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司推出一新款手机,因其功能强大,外观新潮,一上市便受到消费者争相抢购,销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
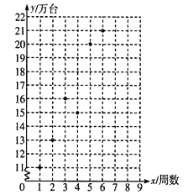
(Ⅰ)根据散点图,用最小二乘法求
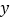 关于
关于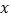 的线性回归方程,并预测该款手机第8周的销量;
的线性回归方程,并预测该款手机第8周的销量;(Ⅱ)为了分析市场趋势,该公司市场部从前6周的销售数据中随机抽取2周的数据,求抽到的这2周的销量均在20万台以下的概率.
参考公式:回归直线方程
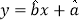 ,其中:
,其中: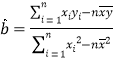 ,
,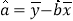 .
.
相关试题

