【题目】一个盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,现进行有放回的连续抽取两次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求条件“取出卡片的号码之和不小于7或小于5”的概率.
参考答案:
【答案】
(1)解:盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,
现进行有放回的连续抽取两次,每次任意地取出一张卡片,
基本事件总数n=5×5=25,
所有可能结果为:
(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5),(3,1),(3,2),(3,3),
(3,4),(3,5),(4,1),(4,2),(4,3),(4,4),(4,5),(5,1),(5,2),(5,3),(5,4),(5,5).
(2)解:“取出卡片的号码之和不小于7或小于5”包含的基本事件有:
(1,1),(1,2),(1,3),(2,1),(2,2),(2,5),(3,1),(3,4),(3,5),
(4,3),(4,4),(4,5),(5,2),(5,3),(5,4),(5,5),共有m=16个,
∴“取出卡片的号码之和不小于7或小于5”的概率p= ![]() =
= ![]()
【解析】(1)先求出基本事件总数n=5×5=25,再利用列举法列出所有可能结果.(2)利用列举法求出“取出卡片的号码之和不小于7或小于5”包含的基本事件个数,由此能求出“取出卡片的号码之和不小于7或小于5”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是偶函数,且f(x+
 )=f(
)=f(  ﹣x),当﹣
﹣x),当﹣  ≤x≤0时,f(x)=(
≤x≤0时,f(x)=(  )x﹣1,记an=f(
)x﹣1,记an=f( 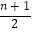 ),n∈N+ , 则a2046的值为( )
),n∈N+ , 则a2046的值为( )
A.1﹣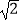
B.1﹣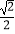
C.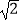 ﹣1
﹣1
D.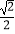 ﹣1
﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}当n≥2时满足
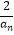 =
= 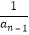 +
+ 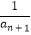 ,且a3a5a7=
,且a3a5a7= 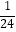 ,
, 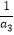 +
+ 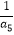 +
+ 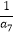 =9,Sn是数列{
=9,Sn是数列{ 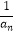 }的前n项和,则S4= .
}的前n项和,则S4= . -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:x>0,x+
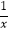 >a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围.
>a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.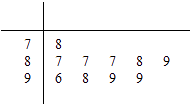
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人, -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.
相关试题

