【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.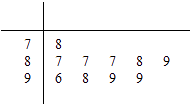
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
参考答案:
【答案】
(1)解:设Ai表示所取3人中有i个人评价该教师为“优秀”,
至多1人评价该教师为“优秀”记为事件A,
则P(A)=P(A0)+P(A1)= ![]() =
= ![]() .
.
(2)解:由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=( ![]() )3=
)3= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)=( ![]() )3=
)3= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =0.9.
=0.9.
【解析】(1)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多1人评价该教师为“优秀”记为事件A,由P(A)=P(A0)+P(A1),能求出至多有1人评价该教师是“优秀”的概率.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}当n≥2时满足
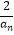 =
= 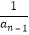 +
+ 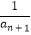 ,且a3a5a7=
,且a3a5a7= 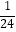 ,
, 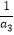 +
+ 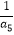 +
+ 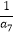 =9,Sn是数列{
=9,Sn是数列{ 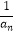 }的前n项和,则S4= .
}的前n项和,则S4= . -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,现进行有放回的连续抽取两次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求条件“取出卡片的号码之和不小于7或小于5”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:x>0,x+
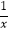 >a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围.
>a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传3月5日学雷锋纪念日,重庆二外在高一,高二年级中举行学雷锋知识竞赛,每年级出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为
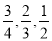 ,乙队每人答对的概率都是
,乙队每人答对的概率都是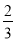 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用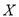 表示甲队总得分.
表示甲队总得分.(1)求随机变量
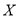 的分布列及其数学期望
的分布列及其数学期望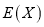 ;
;(2)求甲队和乙队得分之和为4的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
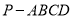 中,
中,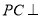 底面
底面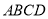 ,底面
,底面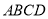 是直角梯形,
是直角梯形,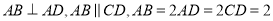 ,
,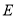 是
是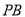 上的点.
上的点.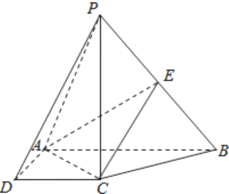
(1)求证: 平面
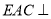 平面
平面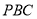 ;
; (2)若
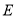 是
是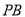 的中点,且二面角
的中点,且二面角 的余弦值为
的余弦值为 ,求直线
,求直线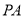 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

