搜索
【题目】在直角坐标系xOy中，圆C的方程为（x﹣ 
）2+（y+1）2=9，以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C的极坐标方程；
（2）直线OP：θ= 
（p∈R）与圆C交于点M，N，求线段MN的长．
参考答案：
【答案】
（1）解：（x﹣ 
）2+（y+1）2=9可化为x2+y2﹣2 x+2y﹣5=0，
故其极坐标方程为ρ2﹣2 ρcosθ+2ρsinθ﹣5=0
（2）解：将θ= 
代入ρ2﹣2 ρcosθ+2ρsinθ﹣5=0，得ρ2﹣2ρ﹣5=0，
∴ρ1+ρ2=2，ρ1ρ2=﹣5，
∴|MN|=|ρ1﹣ρ2|= 
=2 
【解析】（1）利用直角坐标方程化为极坐标方程的方法，求圆C的极坐标方程；（2）利用|MN|=|ρ1﹣ρ2|，求线段MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
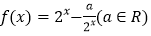，将
的图象向右平移两个单位长度，得到函数
的图象．（1）求函数
的解析式；（2）若方程
在
上有且仅有一个实根，求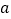
的取值范围；（3）若函数
与的图象关于直线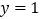
对称，设
，已知
对任意的
恒成立，求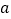的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=（1﹣ax）ln（x+1）﹣bx，其中a和b是实数，曲线y=f（x）恒与x轴相切于坐标原点．
（1）求常数b的值；
（2）当a=1时，讨论函数f（x）的单调性；
（3）当0≤x≤1时关于x的不等式f（x）≥0恒成立，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】设m, n是两条不同的直线,
是三个不同的平面, 给出下列四个命题:①若m⊥α,n∥α,则m⊥n;； ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;； ④若α⊥r, β⊥r,则α∥β．
其中正确命题的序号是 （ ）
A.
①和② B. ②和③ C. ③和④ D. ①和④ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知过原点的动直线l与圆
相交于不同的两点A，B．（1）求线段AB的中点M的轨迹C的方程；
（2）是否存在实数k，使得直线L：y=k（x﹣4）与曲线C只有一个交点？若存在，求出k的取值范围；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
，
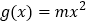，若方程
在
有四个不同的解，则
的取值范围为（ ）A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知f（x）=|x+2|﹣|2x﹣1|，M为不等式f（x）＞0的解集．
（1）求M；
（2）求证：当x，y∈M时，|x+y+xy|＜15．
相关试题
