【题目】如图,四边形![]() 和四边形
和四边形![]() 均是直角梯形,
均是直角梯形,![]() ,二面角
,二面角![]() 是直二面角,
是直二面角,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)见解析(2)![]()
【解析】分析:(1)利用线面、面面平行的判定和性质定理即可证明;
(2)根据条件,建立相应的空间直角坐标系,利用平面的法向量所成角的余弦值来得到对应的二面角的余弦值的大小.
详解:(Ⅰ)由已知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理可得:![]() 平面
平面![]() .
.
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(Ⅱ)因为二面角![]() 是直二面角,
是直二面角,
所以平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() ,有
,有![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ;
;
由已知得,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则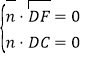 ,即
,即![]() .
.
不妨取![]() ,则
,则![]() ,
,
取面![]() 的一个法向量
的一个法向量![]() ,
,
所以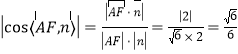 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
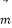 =(2sinx,-1),
=(2sinx,-1),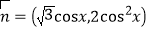 ,函数f(x)=
,函数f(x)=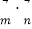 .
.(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
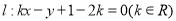 .
.(1)求证:无论
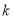 取何值,直线
取何值,直线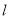 始终经过第一象限;
始终经过第一象限;(2)若直线
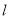 与
与 轴正半轴交于
轴正半轴交于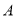 点,与
点,与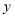 轴正半轴交于
轴正半轴交于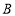 点,
点,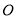 为坐标原点,设
为坐标原点,设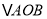 的面积为
的面积为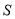 ,求
,求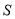 的最小值及此时直线
的最小值及此时直线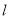 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程.
处的切线方程.(Ⅱ)当
 时,若曲线
时,若曲线 上的点
上的点 都在不等式组
都在不等式组 所表示的平面区域内,试求
所表示的平面区域内,试求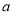 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, ,侧面
,侧面 底面
底面 ,
, ,
, ,
, ,
, 分别为
分别为 ,
, 的中点,点
的中点,点 在线段
在线段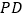 上.
上.(Ⅰ)求证:
 平面
平面 .
.(Ⅱ)若
 为
为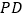 的中点,求证:
的中点,求证: 平面
平面 .
.(Ⅲ)如果直线
 与平面
与平面 所成的角和直线
所成的角和直线 与平面
与平面 所在的角相等,求
所在的角相等,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一年级开设
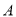 、
、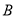 、
、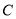 、
、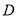 、
、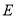 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选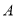 课程,不选
课程,不选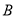 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.(Ⅰ)求甲同学选中
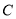 课程且乙同学未选中
课程且乙同学未选中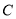 课程的概率.
课程的概率.(Ⅱ)用
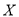 表示甲、乙、丙选中
表示甲、乙、丙选中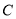 课程的人数之和,求
课程的人数之和,求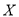 的分布列和数学期望.
的分布列和数学期望.
相关试题

